Dòng chữ trên trang sách được đặt cách thấu kính hội tụ 5 cm cho ảnh ảo có chiều cao gấp đôi. Tìm tiêu cự của thấu kính.
Bước 1. Tóm tắt để bài, ghi các kích thước đã cho.
Bước 2. Vẽ ảnh của vật qua thấu kính. (Các khoảng cách và chiều cao vật cần vẽ theo tỉ lệ thích hợp)
Bước 3. Dựa theo hai cặp tam giác đồng dạng thiết lập các tỉ số.
Bước 4. Giải các phương trình thu được.
Ta có: OA = 5 cm, A’B’ = 2AB. Tìm OF.
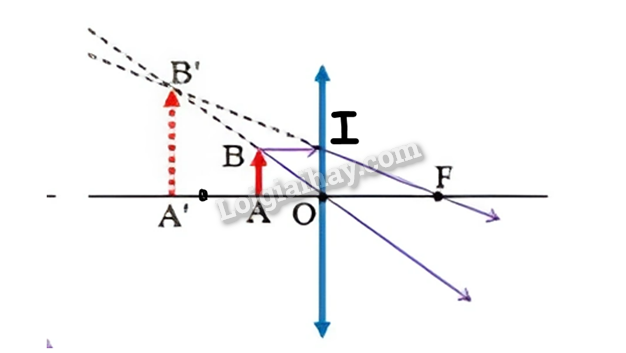
Do ∆ОАВ ~ ∆OA’B’ và ∆FA’B’ ~ ∆FOI
Nên\(\frac{{OA’}}{{OA}} = \frac{{A’B’}}{{AB}}\) \(\)(1) \(\frac{{OF}}{{OA’ + OF}} = \frac{{OI}}{{A’B’}}\) (2) OI=AB (3)
Từ (1), (2) và (3) ta có:
\(\begin{array}{l}\frac{{OF}}{{OA’ + \;OF}} = \frac{{OI}}{{A’B’}} = > \frac{{OF}}{{OA’ + \;OF}} = \frac{{AB}}{{A’B’}} = > \frac{{OF}}{{OA’ + \;OF}} = \frac{{OA}}{{OA’}}\\ = > OF.OA’ = OA.OA’ + OA.OF\\ = > OF(OA’ - OA) = OA.OA’\\ = > \frac{1}{{\;OF}} = \frac{{OA’ - OA}}{{OA’.OA}} = > \frac{1}{{\;OA}} - \frac{1}{{\;OA’}} = \frac{1}{{OF}}\end{array}\)
Mà \(\frac{{OA’}}{{OA}} = \frac{{A’B’}}{{AB}} = 2 = > OA’ = 2OA = 2.5 = 10cm\)
Thay số vào ta được: \(\frac{1}{{\;OA}} - \frac{1}{{\;OA’}} = \frac{1}{{OF}} = > \frac{1}{{\;5}} - \frac{1}{{\;10}} = \frac{1}{{OF}} = > OF = 10cm\)