Câu hỏi/bài tập:
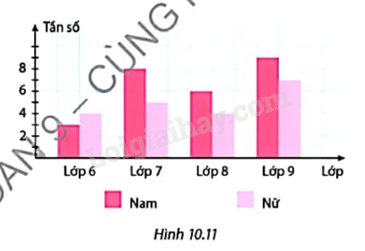
Hình 10.11 là biểu đồ thống kê số học sinh tham gia câu lạc bộ cờ vua. Lấy ngẫu nhiên một học sinh trong số này. Tính xác suất của các biến cố:
a) Lấy được một học sinh nữ lớp 9;
b) Lấy được một học sinh lớp 6;
c) Lấy được một học sinh nam lớp 7 hoặc lớp 8.

Cho A là một biến cố liên quan đến phép thử T. Nếu phép thử T có n kết quả đồng khả năng xảy ra, trong đó có k kết quả thuận lợi cho biến cố A, thì xác suất của biến cố A được tính theo công thức: \(P(A) = \frac{k}{n}\).

Advertisements (Quảng cáo)
Theo biểu đồ tổng số học sinh tham gia câu lạc bộ cờ vua là 46 học sinh. Do đó nếu phép thử là lấy ngẫu nhiên một học sinh trong số đó thì có 46 kết quả có thể xảy ra.
Suy ra không gian mẫu của phép thử là 46 kết quả đồng khả năng.
a) Xét biến cố A: “Lấy được một học sinh nữ lớp 9” có 7 kết quả thuận lợi.
Suy ra \(P(A) = \frac{7}{{46}} = \frac{2}{{23}}\).
b) Xét biến cố B: “Lấy được một học sinh lớp 6” có 7 kết quả thuận lợi.
Suy ra \(P(B) = \frac{7}{{46}} = \frac{2}{{23}}\).
c) Xét biến cố C: “Lấy được một học sinh nam lớp 7 hoặc lớp 8” có 14 kết quả thuận lợi.
Suy ra \(P(C) = \frac{{14}}{{46}} = \frac{7}{{23}}\).
