Bài 12.11 trang 19, 20, 21 SBT Vật lý 10 - Kết nối tri thức: Một cầu thủ bóng rổ cao 2m đứng cách xa rổ 10 m theo phương nằm ngang để tập ném bóng vào rổ...

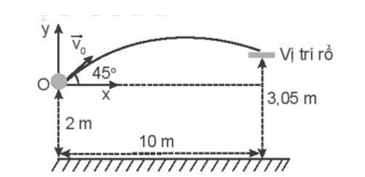
Một cầu thủ bóng rổ cao 2m đứng cách xa rổ 10 m theo phương nằm ngang để tập ném bóng vào rổ. Biết miệng rổ ở độ cao 3,05 m. Hỏi người đó phải ném bóng từ độ cao ngang đầu với vận tốc theo phương 45° có độ lớn bằng bao nhiêu đề bóng rơi vào rổ? Lấy g= 9,8 m/s.

Viết phương trình độ dịch chuyển theo phương Ox và Oy:

d_x = v_0xt; d_y = v_0yt - \(\frac{1}{2}\)gt². Để bóng rơi trúng rổ thì d_x = 10 m, d_y = 1,05 m. Giải phương trình ta tìm được v₀.

Chọn hệ trục tọa độ Oxy như hình vẽ. Ta có:

Theo phương Ox: d_x = v_0xt = v₀t.cos45^o = \(\frac{{\sqrt 2 }}{2}\)v₀t (m)_.

Theo phương Oy: d_y = v_0yt - \(\frac{1}{2}\)gt² = \(\frac{{\sqrt 2 }}{2}\)v₀t – 5t² (m).

Để bóng rơi trúng rổ thì d_x = 10 m, d_y = 1,05 m.

Khi đó: d_x = \(\frac{{\sqrt 2 }}{2}\)v₀t = 10 m => d_y = \(\frac{{\sqrt 2 }}{2}\)v₀t – 5t² = 10 – 5t² = 1,05 m.

=> t = \(\frac{{\sqrt {179} }}{{10}}\)s.

=> v₀ = \(\frac{{10.2}}{{\sqrt 2 .\frac{{\sqrt {179} }}{{10}}}}\)≈ 10,57 m/s.