Câu hỏi/bài tập:
Một vật được ném xiên từ mặt đất với vận tốc ban đầu có độ lớn v0 = 50 m/s. Khi lên tới điểm cao nhất, vận tốc của vật có độ lớn là 40 m/s. Bỏ qua sức cản của không khí, lấy g= 10 m/s2.
a) Xác định góc ném α.
b) Vẽ quỹ đạo chuyển động của vật.
c) Tính tầm cao và tầm xa của vật.

a) Ta có vx = v0cosα => cosα = \(\frac{{{v_x}}}{{{v_{_0}}}}\). Từ đó suy ra góc ném α.
b) Quỹ đạo chuyển động của vật có dạng hình parabol với góc ném được xác định ở câu a).
c) Dựa vào công thức tính tầm bay cao và tầm bay xa của vật được ném xiên:
Tầm cao: H = dymax = \(\frac{{v_{0y}^2}}{{2g}}\) = \(\frac{{v_0^2.{{\sin }^2}\alpha }}{{2g}}\)
Advertisements (Quảng cáo)
Tầm xa: L = dxmax = \(\frac{{v_{0x}^2}}{g}\) = \(\frac{{v_0^2.{{\sin }^2}2\alpha }}{g}\)

a) Tại điểm cao nhất thì vận tốc theo phương thẳng đứng vy = 0.
=> vx = \(\sqrt {{v^2} - v_y^2} \)= \(\sqrt {{{40}^2} - {0^2}} \)= 40 m/s.
Mà ta có vx = v0cosα => cosα = \(\frac{{{v_x}}}{{{v_{_0}}}}\)= \(\frac{{40}}{{50}}\)=> α ≈ 36,87o.
b) Quỹ đạo chuyển động của vật có dạng hình parabol với góc ném được xác định ở câu a) như hình vẽ:
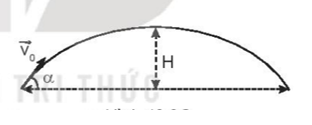
c) Ta có:
Tầm cao: H = \(\frac{{v_0^2.{{\sin }^2}\alpha }}{{2g}}\)= 45 m.
Tầm xa: L= \(\frac{{v_0^2.{{\sin }^2}2\alpha }}{g}\)= 240 m.
