Câu hỏi/bài tập:
Một vật được ném theo phương nằm ngang từ độ cao 4,9 m, có tầm xa trên
mặt đất L= 5 m. Lấy g= 9,8 m/s2
a) Tính vận tốc ban đầu.
b) Viết phương trình chuyển động và vẽ đồ thị độ dịch chuyền – thời gian.
c) Xác định vận tốc của vật ngay trước khi chạm đất.

a) Áp dụng công thức tính tầm xa của vật bị ném: L = v0\(\sqrt {\frac{{2H}}{g}} \).
b) Xác định độ dịch chuyển theo phương thẳng đứng y và độ dịch chuyển theo phương nằm ngang x.
c) Sử dụng công thức tổng hợp vận tốc: v2 = vx2 + vy2
Trong đó: vx = v0; vy = gt.

a) Theo công thức tính tầm xa của vật bị ném: L = v0\(\sqrt {\frac{{2h}}{g}} \)
=> v0 = L\(\sqrt {\frac{g}{{2h}}} \)= 5\(\sqrt {\frac{{9,8}}{{2.4,9}}} \)= 5 m/s.
b) Ta cần xác định được mối quan hệ giữa độ dịch chuyển theo phương thẳng đứng y và độ dịch chuyển theo phương nằm ngang x:
Ta có: x = v0t => t = \(\frac{x}{{{v_0}}}\);
y = h = \(\frac{1}{2}\)gt2 = 4,9 - \(\frac{1}{2}\)g\(\frac{{{x^2}}}{{v_0^2}}\)= 4,9 – 0,196x2
Ta lập bảng biến thiên với 6 giá trị của x và y:
|
x (m) |
0 |
Advertisements (Quảng cáo) 1 |
2 |
3 |
4 |
5 |
|
y (m) |
4,9 |
4,7 |
4,1 |
3,1 |
1,8 |
0 |
Quỹ đạo là \(\frac{1}{2}\)đường parabol như hình vẽ:
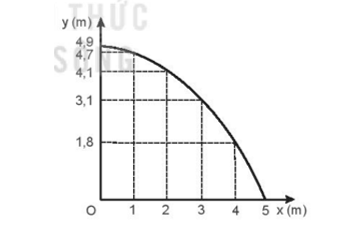
c) Ta có vx = v0 = 5 m/s;
vy = gt = g\(\sqrt {\frac{{2h}}{g}} \)= \(\sqrt {2gh} \)= \(\sqrt {2.9,8.4,9} \)= 9,8 m/s.
Do đó: v =\(\sqrt {{v_x}^2 + {\rm{ }}{v_y}^2} \) =\(\sqrt {{5^2} + {\rm{ 9,}}{{\rm{8}}^2}} \)≈ 11m/s.
Ta có: tanα = \(\frac{{{v_y}}}{{{v_x}}}\)= 1,96 => α ≈ 63o.
Vậy vận tốc của vật ngay trước khi chạm đất có độ lớn là 11 m/s, hướng xuống dưới 63o so với phương nằm ngang.
