Bài 21.9 trang 37, 38, 39 SBT Vật lý 10 - Kết nối tri thức: Một cái thước AB = 1,2 m đặt trên mặt bàn nhẵn nằm ngang...

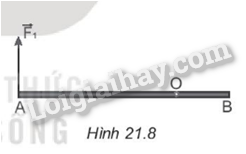
Một cái thước AB = 1,2 m đặt trên mặt bàn nhẵn nằm ngang, có trục quay O cách đầu A một khoảng 80 cm (Hình 21.8). Một lực F₁ = 5 N tác dụng lên đầu A theo phương vuông góc với thước và lực thứ hai tác dụng lên đầu B của thước theo phương vuông góc với thước (không vẽ trên hình). Các lực đều nằm trên mặt phẳng nằm ngang. Nếu thước không chuyển động thì lực tác dụng vào đầu B của thước có hướng và độ lớn như thế nào?

Muốn cho một vật có trục quay cố định ở trạng thái cân bằng, thì tổng các moment lực có xu hướng làm vật quay theo chiều kim đồng hồ phải bằng tổng các moment lực có xu hướng làm vật quay ngược chiều kim đồng hồ.

Áp dụng quy tắc moment lực: \(\sum {M = 0} \)

Trong đó biểu thức moment lực: M = Fd.

OA = 80 cm = 0,8 m; OB = AB – OA = 1,2 – 0,8 = 0,4 m.

Muốn cho một vật có trục quay cố định ở trạng thái cân bằng, thì tổng các moment lực có xu hướng làm vật quay theo chiều kim đồng hồ phải bằng tổng các moment lực có xu hướng làm vật quay ngược chiều kim đồng hồ.

Chọn chiều (+) là chiều kim đồng hồ.

Ta có 2 lực ở 2 bên so với trục quay. Thước không chuyển động nên:

Áp dụng quy tắc moment lực: \(\sum {M = 0} \) => M₍\({F_1}\)₎ = M₍\({F_2}\)₎ => F₁.OA = F₂.OB

=> F₂ = \(\frac{{{F_1}.OA}}{{OB}}\)= \(\frac{{5.0,8}}{{0,4}}\)= 10 N.

Vậy F₂ = 10 N, \(\overrightarrow {{F_2}} \)cùng hướng \(\overrightarrow {{F_1}} \)