Bài 4.9 trang 7, 8 SBT Vật lý 10 - Kết nối tri thức: Vị trí điểm tới cách điểm đối diện với điểm khởi hành của người bơi là bao nhiêu mét?...

Một người bơi từ bờ này sang bờ kia của một con sông rộng 50m theo hướng vuông góc với bờ sông. Do nước sông chảy mạnh nên quãng đường người đó bơi gấp 2 lần so với khi bơi trong bể bơi.

a) Hãy xác định độ dịch chuyển của người này khi bơi sang bờ sông bên kia.

b) Vị trí điểm tới cách điểm đối diện với điểm khởi hành của người bơi là bao nhiêu mét?

Sử dụng Phương pháp giải tổng hợp độ dịch chuyển.

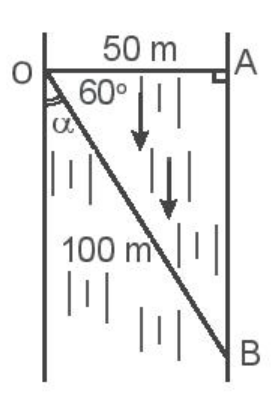
a) Do nước sông chảy mạnh nên quãng đường người đó bơi trên sông gấp 2 lần khi bơi trong bể bơi có nước đứng yên.

⇨ OB = 2OA = 100 m

⇨ Độ dịch chuyển d = OB = 100 m

Ta có: cos\(\widehat {AOB}\) = \(\frac{{OA}}{{OB}} = \frac{{50}}{{100}} = \frac{1}{2}\)=> \(\widehat {AOB}\) = 60^o

⇨ ∝ = 90^o – 60^o = 30^o

Người này dịch chuyển theo hướng hợp với bờ sông một góc 30^o.

b) Ta có điểm khởi hành là O, điểm đối diện O là A, điểm tới là B.

Vị trí điểm tới cách điểm đối diện với điểm khởi hành của người bơi là:

AB = \(\sqrt {O{B^2} - O{A^2}} \)= \(\sqrt {{{100}^2} - {{50}^2}} \)≈ 86,6 m.