Câu hỏi/bài tập:
Dựa vào đồ thị ở Hình 7.3, xác định:
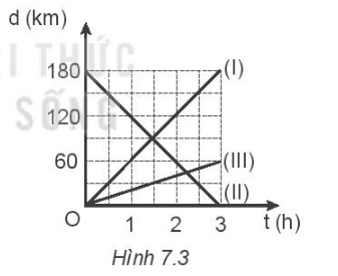
a) Vận tốc của mỗi chuyển động.
b) Phương trình của mỗi chuyển động.
c) Vị trí và thời điểm các chuyển động gặp nhau.

Sử dụng cách đọc số liệu từ đồ thị xác định d0 và d tại một thời điểm t bất kì.
Sử dụng công thức tính vận tốc và phương trình của chuyển động thẳng đều:
v = \(\frac{{\Delta d}}{{\Delta t}}\); d = d0 + vt
Để xác định vị trí và thời gian các chuyển động gặp nhau ta cho phương trình của các chuyển động bằng nhau.

a)
Chuyển động (I):
Tại thời điểm t0 = 0, d0 = 0 km;
Tại thời điểm t1 = 3 h, d1 = 180 km;
Ta có vận tốc của chuyển động (I) là: v1 = \(\frac{{\Delta d}}{{\Delta t}}\)= \(\frac{{{d_1} - {d_0}}}{{{t_1} - {t_0}}}\)= \(\frac{{180 - 0}}{{3 - 0}}\)= \(\frac{{180}}{3}\)= 60 km/h
Chuyển động (II):
Advertisements (Quảng cáo)
Tại thời điểm t0 = 0, d0 = 180 km;
Tại thời điểm t1 = 3 h, d1 = 0 km;
Ta có vận tốc của chuyển động (II) là: v2 = \(\frac{{\Delta d}}{{\Delta t}}\)= \(\frac{{{d_1} - {d_0}}}{{{t_1} - {t_0}}}\)= \(\frac{{0 - 180}}{{3 - 0}}\)= \(\frac{{ - 180}}{3}\)= -60 km/h
Chuyển động (III):
Tại thời điểm t0 = 0, d0 = 0 km;
Tại thời điểm t1 = 3 h, d1 = 60 km;
Ta có vận tốc của chuyển động (II) là: v3 = \(\frac{{\Delta d}}{{\Delta t}}\)= \(\frac{{{d_1} - {d_0}}}{{{t_1} - {t_0}}}\)= \(\frac{{60 - 0}}{{3 - 0}}\)= \(\frac{{60}}{3}\)= 20 km/h
b)
Phương trình chuyển động có dạng: d = do + vt.
Phương trình chuyển động (I) có dạng: d1 = do1 + v1t = 0 + 60t = 60t (km).
Phương trình chuyển động (II) có dạng: d2 = do2 + v1t = 180 – 60t (km).
Phương trình chuyển động (III) có dạng: d3 = do3 + v1t = 0 + 20t = 20t (km).
c) Chuyển động (I) gặp (II) khi d1 = d2 \( \Leftrightarrow \) 60t = 180 – 60t \( \Leftrightarrow \) t = 1,5 h
=> d1 = 90 km
Chuyển động (II) gặp (III) khi d2 = d3 \( \Leftrightarrow \) 180 - 60t = 20t \( \Leftrightarrow \) t = 2,25 h
=> d1 = 45 km
Vậy (I) và (II) gặp nhau tại thời điểm 1,5h, cách điểm khởi hành của (I) 90 km.
(II) và (III) gặp nhau tại thời điểm 2,25h, cách điểm khởi hành của (II) 45 km.
