Bài 9.10 trang 15, 16, 17 SBT Vật lý 10 - Kết nối tri thức: Một xe đạp đang đi với vận tốc 2 m/s thì xuống dốc chuyển động nhanh dần đều với gia tốc 0,2 m/s2...

Một xe đạp đang đi với vận tốc 2 m/s thì xuống dốc chuyển động nhanh dần đều với gia tốc 0,2 m/s². Cùng lúc đó, một ô tô đang chạy với vận tốc 20 m/s lên dốc, chuyển động chậm dần đều với gia tốc 0,4 m/s². Xác định vị trí hai xe gặp nhau trên dốc. Biết dốc dài 570 m.

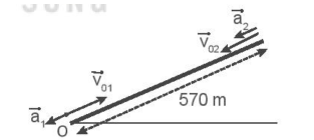
Chọn chiều từ chân dốc lên đỉnh dốc là chiều dương. Điểm O là chân dốc như hình vẽ.

Viết phương trình chuyển động của mỗi xe theo công thức: \(d = {d_0} + {v_0}t + \frac{1}{2}a{t^2}\)

Hai xe gặp nhau khi d₁ = d₂. Giải phương trình ta sẽ xác định được vị trí 2 xe gặp nhau.

Chọn chiều từ chân dốc lên đỉnh dốc là chiều dương. Điểm O là chân dốc như hình vẽ.

Xét chuyển động của ô tô, ta có: v₀₁ = 20 m/s; a₁ = -0,4 m/s².

=> Phương trình chuyển động của ô tô: \({d_1} = {d_{01}} + {v_{01}}t + \frac{1}{2}{a_1}{t^2}\)= 20t – 0,2t². (1)

Xét chuyển động của xe đạp, ta có: v₀₂ = -2 m/s; d₀₂ = 570 m; a₂ = -0,2 m/s².

Phương trình chuyển động: \({d_2} = {d_{02}} + {v_{02}}t + \frac{1}{2}{a_2}{t^2}\)= 570 – 2t – 0,1t². (2)

Khi ô tô và xe đạp gặp nhau: d₁ = d₂ => 20t – 0,2t² = 570 – 2t – 0,1t² (3)

Nghiệm của phương trình (3) là t₁ = 30 s và t₂ = 190 s.\(\)

Thế t₁ vào (1) ta được d₁ = 420 m.

Thế t₂ vào (2) ta được d₂ = - 3400 m (Loại vì 2 xe gặp nhau trên dốc).

Vậy 2 xe gặp nhau tại vị trí cách chân dốc 420 m.