Câu hỏi/bài tập:
Hai vật A và B chuyển động cùng chiều trên đường thẳng có đồ thị vận tốc – thời gian vẽ ở Hình 9.2. Biết ban đầu hai vật cách nhau 78 m.
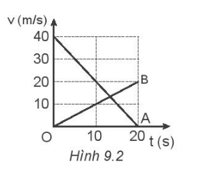
a) Hai vật có cùng vận tốc ở thời điểm nào?
b) Viết phương trình chuyển động của mỗi vật.
c) Xác định vị trí gặp nhau của hai vật.

a) Viết phương trình vận tốc của mỗi vật theo công thức: v = v0 + at
Hai vật có cùng vật tốc khi vA = vB. Giải phương trình sẽ tìm được thời điểm hai vật có cùng vật tốc.
b) Viết phương trình chuyển động của mỗi vật theo công thức: \(d = {d_0} + {v_0}t + \frac{1}{2}a{t^2}\).
c) Hai vật gặp nhau khi dA = dB. Giải phương trình sẽ tìm được vị trí gặp nhau của 2 vật.

a) Từ đồ thị ta viết được phương trình vận tốc của mỗi vật như sau:
vA = v0A + a1t = 40 – 2t (m/s).
Advertisements (Quảng cáo)
vB = v0B + a2t = t
Hai vật có cùng vận tốc khi vA = vB ⬄ 40 – 2t = t ⬄ t = \(\frac{{40}}{3}\)≈13,3 s.
b) Chuyển động A có:
v01 = 40 m/s; a1 = \(\frac{{0 - 40}}{{20}}\)= -2 m/s2.
=> \({d_A} = {d_{01}} + {v_{01}}t + \frac{1}{2}{a_1}{t^2}\)= 40t – t2 (1)
- Chuyển động B có:
v02 = 0 m/s; a2 = \(\frac{{10 - 0}}{{10}}\)= 1 m/s2.
=> \({d_B} = {d_{02}} + {v_{02}}t + \frac{1}{2}{a_2}{t^2}\)= \(78 + \frac{1}{2}{t^2}\). (2)
c) Hai vật gặp nhau khi dA = dB ⬄ 40t – t2 = \(78 + \frac{1}{2}{t^2}\) (3)
Phương trình (3) cho hai nghiệm t = 2,12 s và t’ = 24,5 s
Loại t’vì t’ lớn hơn 20 s.
Thế t vào (1) ta được dA = 81,5 m.
Vậy hai vật gặp nhau cách vị trí ban đầu của A 81,5 m.
