Câu hỏi/bài tập:
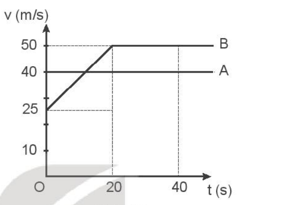
Hình II.3 là đồ thị vận tốc – thời gian của hai ô tô A và B cùng chạy theo một hướng trong 40 s. Xe A vượt qua xe B tại thời điểm t = 0. Để bắt kịp xe A, xe B tăng tốc trong 20 s để đạt vận tốc 50 m/s.
a) Tính độ dịch chuyển của xe A trong 20s.
b) Tính gia tốc của xe B trong 20 s.
c) Sau bao lâu thì xe B đuổi kịp xe A.
d) Tính quãng đường mỗi xe đi được trong 40 s và khi hai xe gặp nhau.

a) Ta thấy xe A chuyển động thẳng đều nên dA = vAtA.
b) Sử dụng công thức tính gia tốc: a = \(\frac{{\Delta {v_B}}}{{\Delta t}}\).
c) Viết phương trình chuyển động của xe B:
dB = dB1 + dB2 = v0Bt + \(\frac{1}{2}\)atB2 + vB(tB – 20)
Hai xe gặp nhau khi dA = dB.
d) Thay số vào phương trình độ dịch chuyển của mỗi xe.

a) Hai xe chuyển động thẳng không đổi chiều nên d = s và v =ϑ.
Advertisements (Quảng cáo)
Ta có xe A chuyển động thẳng đều nên dA = vAtA = 40.20 = 800 m.
b) Gia tốc của xe B trong 20 s là: a = \(\frac{{\Delta {v_B}}}{{\Delta t}}\)= \(\frac{{50 - 25}}{{20}}\)= 1,25 m/s2.
c)
Ta có: dA = vAt = 40t (1)
dB = dB1 + dB2.
Mà dB1 = v0BtB + \(\frac{1}{2}\)atB2 = 25.20 + \(\frac{1}{2}\).1,25.202 = 750 m.
=> Trong 20 s đầu 2 xe chưa gặp nhau.
Có dB2 = vB(t – 20) = 50(t – 20).
=> dB = 750 + 50(t – 20). (2)
Khi B đuổi kịp A thì dA = dB ⬄ 40t = 750 + 50(t – 20) => t = 25 s.
d) Quãng đường xe A đi được trong 40 s là: dA = vAt = 40t = 40.40 = 1600 m.
Quãng đường xe B đi được trong 40 s là:
dB = 750 + 50(t – 20) = 750 + 50(40 – 20) = 1750 m.
Thế t = 25 s vào (1), (2) ta được:
Khi hai xe gặp nhau, hai xe đi được quãng đường là dA = dB = 1000 m.
