II.6 trang 22, 23, 24 SBT Vật lý 10 - Kết nối tri thức: Một cầu thủ tennis ăn mừng chiến thắng bằng cách đánh quả bóng lên trời theo phương thẳng đứng với vận tốc lên tới 30...

Một cầu thủ tennis ăn mừng chiến thắng bằng cách đánh quả bóng lên trời theo phương thẳng đứng với vận tốc lên tới 30 m/s. Bỏ qua sức cản của không khí và lấy g =10 m/s².

a) Tính độ cao cực đại mà bóng đạt được.

b) Tính thời gian từ khi bóng đạt độ cao cực đại tới khi trở về vị trí được đánh lên.

c) Tính vận tốc của bóng ở thời điểm t = 5s kể từ khi được đánh lên.

d) Vẽ đồ thị vận tốc - thời gian và gia tốc - thời gian của chuyển động của bóng.

a) Sử dụng công thức liên hệ giữa vận tốc, gia tốc và quãng đường: v² – v₀² = 2gh

=> h = -\(\frac{{v_0^2}}{{2g}}\).

b) Thời gian từ khi bóng đạt độ cao cực đại tới khi trở về vị trí được đánh lên bằng thời gian bóng rơi từ độ cao cực đại về vị trí ban đầu.

Áp dụng công thức: \(v = {v_0} + gt\) => t.

c) Sử dụng công thức tính vận tốc: \(v = {v_0} + gt\).

d) Từ các dữ kiện thu được, vẽ đồ thị vận tốc - thời gian và gia tốc - thời gian của chuyển động của bóng

Chọn hệ trục tọa độ có gốc O là vị trí bóng tiếp xúc với vợt và bắt đầu chuyển động, chiều dương là chiều từ dưới lên (Oy) và chiều từ trái sang phải (Ox).

a) Độ cao cực đại mà bóng đạt được là:

Ta sử dụng công thức liên hệ giữa vận tốc, gia tốc và quãng đường:

\({v_y}^2-{\rm{ }}{v_{0y}}^2 = {\rm{ }}2gh\) => h = -\(\frac{{v_{0y}^2}}{{2g}}\)= 45 m.

b) Thời gian từ khi bóng đạt độ cao cực đại tới khi trở về vị trí được đánh lên bằng thời gian bóng rơi từ độ cao cực đại về vị trí ban đầu.

Tại vị trí bóng đạt độ cao cực đại: v_y = 0.

Ta có: \({v_y} = {v_{0y}} + gt = 0\) => t = -\(\frac{{{v_{0y}}}}{g}\)= 3 s.

c)

Vì từ khi được đánh lên bóng mất 3s để đạt độ cao cực đại nên tại thời điểm t = 5s, bóng đang rơi xuống.

Vận tốc của bóng ở thời điểm t = 5s kể từ khi được đánh lên là:

v₅ = v_0y + gt₅ = 30 + (-10).5 = -20 m/s.

d)

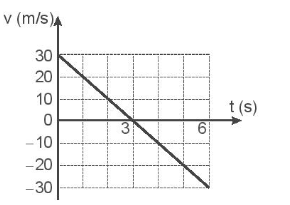
- Đồ thị vận tốc - thời gian

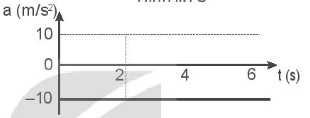
- Đồ thị gia tốc - thời gian