Câu hỏi/bài tập:
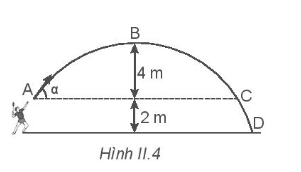
Hình II.4 vẽ quỹ đạo của một quả cầu lông được đánh lên với vận tốc ban đầu v0 = 10 m/s ở độ cao 2 m so với mặt đất. Bỏ qua sức cản của không khí và lấy g = 9,8 m/s2.
a) Xác định độ lớn của góc α.
b) Xác định vận tốc của quả cầu ở vị trí B.
c) Tính khoảng cách giữa vị trí rơi chạm đất của quả cầu và vị trí đứng của
người đánh cầu.

Chọn hệ trục tọa độ.
a) Vận dụng công thức: vyB2 – v0y2 = 2gh1.
Khi đạt độ cao cực đại thì vyB = 0. Chiếu v0y lên hệ trục ta đươc:
=> -v02sin2α = 2gh1 => sin\(\alpha \)=> α.
b) Tổng hợp vận tốc ta có: \(\overrightarrow {{v_B}} = {\overrightarrow v _{xB}} + {\overrightarrow v _{yB}}\). Chiếu lên hệ tọa độ, thay số để tìm được vB.
c) Khoảng cách giữa vị trí rơi chạm đất của quả cầu và vị trí đứng của người đánh cầu = tổng khoảng cách giữa vị trí người đánh cầu đến vị trí quả cầu đạt độ cao cực đại và vị trí quả cầu đạt độ cao cực đại đến khi quả cầu chạm đất:
Advertisements (Quảng cáo)
L = L1 + L2 = vxt1 + vxt2.

Chọn hệ trục tọa độ Oxy có gốc tại vị trí quả cầu tiếp xúc với vợt và được đánh lên, chiều dương hướng lên trên (Oy) và từ trái sang phải (Ox), gốc thời gian t = 0 là lúc đánh quả cầu.
a) Khi đạt độ cao cực đại thì vyB = 0.
vyB2 – v0y2 = 2gh1 => -v02sin2α = 2gh1
=> sinα = \(\sqrt {\frac{{2.9,8.4}}{{{{10}^2}}}} \)= 0,885 => α ≈ 62o
b) Ta có chuyển động của quả cầu là tổng hợp của 2 loại chuyển động: chuyển động theo phương thẳng đứng và chuyển động theo phương nằm ngang.
Do đó, tổng hợp vận tốc của chuyển động, ta được:
\(\overrightarrow {{v_B}} = {\overrightarrow v _{xB}} + {\overrightarrow v _{yB}}\)
=> vB = v0cosα + 0 ≈ 4,7 m/s.
c) L = L1 + L2 = vxt1 + vxt2 = vx(t1 + t2).
Thời gian t1 bằng thời gian để quả cầu chuyển động từ A tới B. Do đó:
t1 = \(\sqrt {\frac{{2{h_1}}}{g}} \)= \(\sqrt {\frac{{2.4}}{{9,8}}} \)= 0,9
Thời gian t2 bằng thời gian để quả cầu rơi từ độ cao B tới mặt đất:t2 = \(\sqrt {\frac{{2{h_2}}}{g}} \)= \(\sqrt {\frac{{2.(4 + 2)}}{{9,8}}} \)= 1,1 S.Do đó: L = 4,7.(0,9 + 1,1) = 9,4 m.
