II.9 trang 22, 23, 24 SBT Vật lý 10 - Kết nối tri thức: Một con tàu chiến ở bên này ngọn núi trên một hòn đảo...

Một con tàu chiến ở bên này ngọn núi trên một hòn đảo, bắn một viên đạn với vận tốc ban đầu 250 m/s theo phương nghiêng góc 75° so với mặt nước biển tới đích là một con tàu khác nằm ở phía bên kia ngọn núi. Biết vị trí của hai con tàu và độ cao của ngọn núi được mô tả như Hình II.5. Hỏi viên đạn có qua được đỉnh núi không và có rơi trúng con tàu kia không?

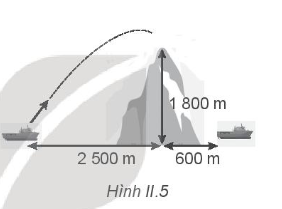
Để xác định xem viên đạn có bay được qua đỉnh núi hay không, ta tính độ cao viên đạt đạt được tại vị trí đỉnh núi.

Viết phương trình chuyển động của viên đạn theo phương Ox, Oy:

x = v_0x.t; y = v_0y + \(\frac{1}{2}g{t^2}\).

Khoảng cách đến đỉnh núi = 2500 m => x = 2500 => Tìm ra t. Thế t vào y, ta tìm được độ cao mà viên đạn đạt được.

Để xác định viên đạn có rơi trúng con tàu kia không, ta xác định tầm bay xa của viên đạn bằng công thức: L = d_xmax = \(\frac{{v_0^2{{\sin }^2}\alpha }}{g}\)

Chọn hệ trục tọa độ Oxy như hình vẽ:

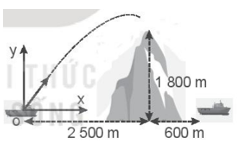
Ta có phương trình chuyển động của viên đạn:

Theo phương Ox:

x = v₀tcosα = (250.cos75^o).t

Theo phương Oy:

y = v₀tsinα - \(\frac{1}{2}\)gt² = (250.sin75^o)t - \(\frac{1}{2}\).10.t²

Để xác định xem viên đạn có bay qua được đỉnh núi hay không, ta thay x = 2500 = (250.cos75^o).t => t ≈ 38,64 s.

=> y = (250.sin75^o)t - \(\frac{1}{2}\).10.t² ≈ 1865,6 m. Vậy viên đạn bay qua được đỉnh núi.

Tầm bay xa của viên đạn: L = \(\frac{{v_0^2\sin 2\alpha }}{g}\)= \(\frac{{{{250}^2}.\sin ({{2.75}^o})}}{{10}}\)= 3125 m.

Viên đạn không bắn trúng tàu.