Hướng dẫn giải bài 5.15 trang 88 SGK Toán lớp 10 tập 1 Kết nối tri thức. Bài 13: Các số đặc trưng đo xu thế trung tâm
![]()
Mẫu số liệu sau đây cho biết cân nặng của 10 trẻ sơ sinh (đơn vị kg):
2,977 3,155 3,920 3,412 4,236
2,593 3,270 3,813 4,042 3,387.
Hãy tìm khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn cho mẫu số liệu này.
![]()
Sắp xếp các giá trị của số liệu trên theo thứ tự từ bé đến lớn là:
2,593; 2,977; 3,155; 3,270; 3,387; 3,412; 3,813; 3,920; 4,042; 4,236. .
Ta có giá trị lớn nhất là 4,236 kg và giá trị nhỏ nhất là 2,593 kg.
Advertisements (Quảng cáo)
Khi đó khoảng biến thiên là: R = 4,236 – 2,593 = 1,643.
Vì n = 10 là số chẵn nên trung vị là trung bình cộng của hai giá trị chính giữa: Q2 = (3,387 + 3,412):2 = 3,3995.
Nửa số liệu bên trái gồm 5 số liệu là một số lẻ nên tứ phân vị thứ nhất là: Q1 = 3,155.
Nửa số liệu bên phải gồm 5 số liệu là một số lẻ nên tứ phân vị thứ ba là: Q3 = 3,920.
Khoảng tứ phân vị là:
∆Q = Q3 – Q1 = 3,920 – 3,155 = 0,765.
Số trung bình cộng của mẫu số liệu là:
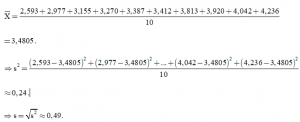
Vậy khoảng biến thiên R = 1,643, khoảng tứ phân vị ∆Q = 0,765; độ lệch chuẩn s ≈ 0,49.
