Câu hỏi trang 52 >Luyện tập - Vận dụng - CH 4
Câu hỏi trang 53 >CH 5 - Bài tập 1 - Bài tập 2
Câu hỏi trang 50 Mở đầy
|
Chuyển động ném là một chuyển động thường gặp trong cuộc sống như: máy bay trực thăng thr những thùng hàng cứu trợ (Hình 9.1a), vận động viên đẩy tạ (Hình 9.1b). Trong cả hai trường hợp, vật đều được ném từ một độ cao h so với mặt đất và có vận tốc đầu \(\overrightarrow {{v_0}} \) hợp với phương ngang một góc α ( 0 ≤ α ≤ 900 ). Để thùng hàng rơi trúng vị trí cần thiết, quả tạ bay đi được quãng đường xa nhất, cần phải có những điều kiện gì?
|

Liên hệ thực tế

Để thùng hàng rơi trúng vị trí cần thiết, quả tạ bay được quãng đường xa nhất thì cần phải có điều kiện: quỹ đạo của vật được ném đúng tầm, đúng độ cao
Câu hỏi trang 50 CH 1
|
1. Quan sát kết quả thí nghiệm trong Hình 9.2 và nhận xét về chuyển động của hai viên bi.
|

Quan sát hình vẽ

Chuyển động của viên bi vàng là chuyển động cong, chuyển động của viên bị đỏ là chuyển động thẳng.
Câu hỏi trang 51 CH 2
|
2. Lập luận để rút ra các phương trình mô tả quỹ đạo chuyển động, thời gian rơi và tầm xa của vật được ném ngang. |

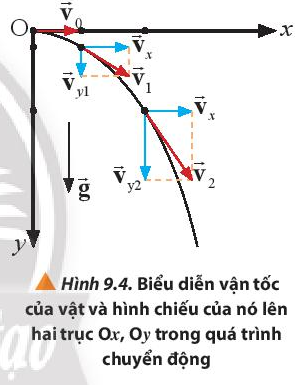
Xét chuyển động ném ngang trong mặt phẳng, vật luôn có gia tốc rơi tự do \(\overrightarrow g \) thẳng đứng hướng xuống và vuông góc với vận tốc ban đầu \(\overrightarrow {{v_0}} \)
Chọn hệ trục tọa độ Oxy như Hình 9.4, gốc thời gian là lúc thả vật
* Trên trục Ox:
- Gia tốc: ax = 0 nên vật chuyển động thẳng đều trên Ox.
- Vận tốc: vx = v0 là hằng số.
- Phương trình chuyển động: x = v0 .t.
* Trên trục Oy:
- Gia tốc: ay = g là hằng số nên vật chuyển động nhanh dần đều trên Oy
- Vận tốc: vy = g.t
- Phương trình chuyển động: \(y = \frac{1}{2}g{t^2}\)
Câu hỏi trang 51 CH 4
|
3. Phân biệt phương trình chuyển động và phương trình quỹ đạo |

Phương trình chuyển động là phương trình vật thay đổi vị trí theo thời gian
+ Phương trình chuyển động trên trục Ox: x = v0 .t.
+ Phương trình chuyển động trên trục Oy: \(y = \frac{1}{2}g{t^2}\)
Phương trình quỹ đạo là phương trình mô tả hình dạng chuyển động của vật, tọa độ của y thay đổi theo x.
\(y = \frac{g}{{2.v_0^2}}.{x^2}\)
Câu hỏi trang 52 Luyện tập
|
Từ một vách đá cao 10 m so với mặt nước biển, một bạn ném ngang một hòn đá nhỏ với tốc độ 5 m/s. Bỏ qua lực cản của không khí và lấy g = 9,81 m/s2 . a) Lập các phương trình chuyển động của hòn đá. b) Xác định tọa độ của hòn đá sau 1 giây. c) Xác định vị trí và tốc độ của hòn đá ngay trước khi hòn đá chạm mặt nước biển. |

Phương trình chuyển động của vật:
+ Phương trình chuyển động trên trục Ox: x = v0 .t.
+ Phương trình chuyển động trên trục Oy: \(y = \frac{1}{2}g{t^2}\)
Tốc độ của vật trước khi vật chạm đất: \(v = \sqrt {2gh} \)

Ta có: v0 = 5 m/s, h = 10 m.
a) Phương trình chuyển động của hòn đá là:
+ Ox: x = v0 .t = 5.t
+ Oy: \(y = \frac{1}{2}g{t^2} = \frac{1}{2}.9,81.{t^2} = 4,905{t^2}\)
b) Tọa độ của hòn đá sau 1 s là:
x = 5.t = 5.1 = 5 (m)
\(y = 4,905{t^2} = 4,{905.1^2} = 4,905(m)\)
c) Thời gian rơi của vật: \(t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.10}}{{9,81}}} \approx 2(s)\)
Vị trí của hòn đá ngay trước khi hòn đá chạm mặt nước biển:
\(y = 4,905.{t^2} = 4,{905.2^2} = 19,62(m)\)
Advertisements (Quảng cáo)
Tốc độ của hòn đá trước khi chạm mặt nước biển là:
\(v = \sqrt {2gh} = \sqrt {2.9,81.10} \approx 14(m/s)\)
Câu hỏi trang 52 Vận dụng
|
Dựa vào kinh nghiệm trong đời sống và các phương trình chuyển động ném ngang, em hãy nêu những yếu tố ảnh hưởng đến tầm xa. Từ đó, phân tích cách thức tăng tầm xa khi ném ngang một vật. |

Liên hệ thực tế.

Những yếu tố ảnh hưởng đến tầm xa:
+ Vận tốc ném ban đầu
+ Độ cao so với mặt đất
+ Vị trí địa lý tại nơi ném (ảnh hưởng đến gia tốc trọng trường).
=> Cách thức tăng tầm xa khi ném ngang:
+ Tăng vận tốc ném ban đầu
+ Tăng độ cao ném so với mặt đất
Câu hỏi trang 52 CH 4
|
4. Khi quả tạ được ném từ độ cao h sao cho vận tốc ban đầu \(\overrightarrow {{v_0}} \) hợp với phương ngang một góc α, hãy dự đoán các yếu tố ảnh hưởng đến tầm xa của quả tạ.
|

Thực hiện thí nghiệm và đưa ra dự đoán

Yếu tố ảnh hưởng đến tầm xa của quả tạ:
+ Góc ném
+ Vận tốc ném ban đầu
+ Độ cao ném
+ Lực cản của không khí
Câu hỏi trang 53 CH 5
|
5. Nêu những lưu ý khi làm thí nghiệm khảo sát để thu được kết quả chính xác nhất có thể. |

Lưu ý khi làm thí nghiệm khảo sát để thu được kết quả chính xác nhất:
+ Lựa chọn vật nặng có kích thước nhỏ để làm vật ném
+ Sử dụng dụng cụ có thể thay đổi góc bắn hoặc độ cao vật nhưng vẫn đảm bảo vận tốc ban đầu có độ lớn không đổi.
Câu hỏi trang 53 Bài tập 1
|
1. Một máy bay đang bay ở độ cao 5 km với tốc độ 500 km/h theo phương ngang thì thả rơi một vật. Hỏi người lái bay phải thả vật cách mục tiêu bao xa theo phương ngang để vật rơi trúng mục tiêu? Lấy g = 9,8 m/s2 . |

Biểu thức tính tầm xa: \(L = {v_0}.\sqrt {\frac{{2h}}{g}} \)
Lời giải chi tiết:
Ta có:
v0 = 500 km/h = 138,89 m/s
h = 5 km = 5000 m
Người lái máy bay phải thả vật cách mục tiêu là: \(L = {v_0}.\sqrt {\frac{{2h}}{g}} = 138,89.\sqrt {\frac{{2.5000}}{{9,8}}} \approx 4436,68(m)\)
Câu hỏi trang 53 Bài tập 2
|
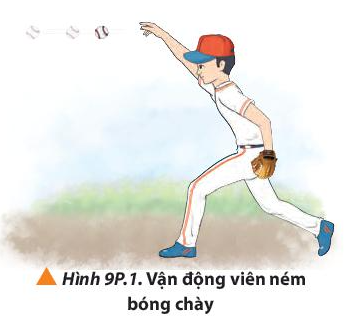
2. Một vận động viên ném một quả bóng chày với tốc độ 90 km/h từ độ cao 1,75 m (Hình 9P.1). Giả sử quả bóng chày được ném ngang, lực cản của không khí là không đáng kể là lấy g = 9,8 m/s2 . a) Viết phương trình chuyển động của quả bóng chày theo hai trục Ox, Oy. b) Quả bóng chày đạt tầm xa bao nhiêu? Tính tốc độ của nó trước khi chạm đất.
|

Phương trình chuyển động của vật:
+ Phương trình chuyển động trên trục Ox: x = v0 .t.
+ Phương trình chuyển động trên trục Oy: \(y = \frac{1}{2}g{t^2}\)
Tốc độ của vật trước khi vật chạm đất: \(v = \sqrt {2gh} \)
Biểu thức tính tầm xa: \(L = {v_0}.\sqrt {\frac{{2h}}{g}} \)

a) Ta có v0 = 90 km/h = 25 m/s; h = 1,75 m.
Phương trình chuyển động của vật:
+ Ox: x = v0 .t = 25.t (m)
+ Oy: \(y = \frac{1}{2}g{t^2} = \frac{1}{2}.9,8.{t^2} = 4,9.{t^2}\)(m)
b) Tầm xa của quả bóng là: \(L = {v_0}.\sqrt {\frac{{2h}}{g}} = 25.\sqrt {\frac{{2.1,75}}{{9,8}}} \approx 14,94(m)\)
Tốc độ của quả bóng trước khi chạm đất: \(v = \sqrt {2.g.h} = \sqrt {2.9,8.1,75} \approx 5,86(m/s)\)