Câu hỏi trang 26 >CH 4 - CH 5
Câu hỏi trang 27 >Luyện tập - CH 6
Câu hỏi trang 28 >Luyện tập - CH 7 Câu hỏi trang 29
Câu hỏi trang 30 >Luyện tập - Vận dụng
Câu hỏi trang 31 >Bài tập 1 - Bài tập 2
Câu hỏi trang 24 MĐ
|
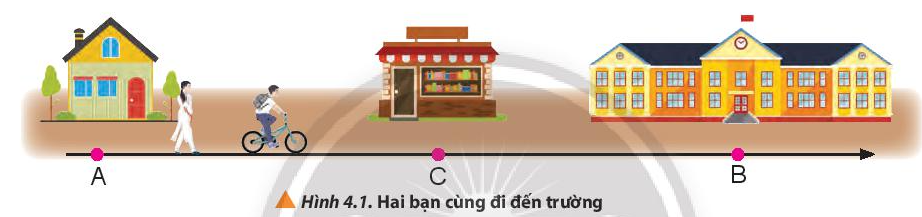
Hai bạn đều xuất phát từ cùng một vị trí để đi đến lớp học (Hình 4.1), một bạn đi bộ và một bạn đi xe đạp. Mặc dù đi chậm hơn nhưng bạn đi bộ lại đến lớp trước bạn đi xe đạp do bạn đi xe đạp dừng lại ở hiệu sách để mua bút và tài liệu học tập. Điều này được lí giải như thế nào theo góc độ vật lí?
|

Vận dụng kiến thức về chuyển động thẳng đã học ở KHTN 7

Quãng đường hai bạn đi được là như nhau, nhưng do bạn đi xe đạp sử dụng thời gian nhiều hơn bạn đi bộ nên bạn đi xe đạp đến lớp muộn hơn.
Câu hỏi trang 24 CH 1
|
1. Vị trí và tọa độ của một vật có phụ thuộc vào vật làm gốc không? Cho một ví dụ trong thực tiễn để minh họa cho câu trả lời của em. |

Liên hiệ thực tiễn

Vị trí và tọa độ của một vật có phụ thuộc vào vật làm gốc.
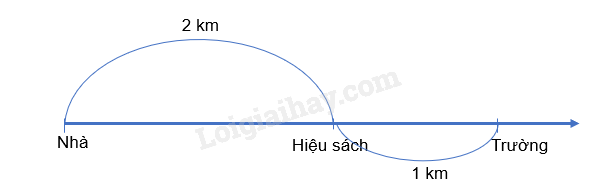
Ví dụ: Từ nhà tới hiệu sách là 2 km, từ hiệu sách đến trường là 1 km. Nếu chọn gốc tại nhà thì tọa độ của hiệu sách là 2 km, của trường là 3 km. Nếu chọn gốc tại hiệu sách thì tọa độ của trường là 1 km, của nhà là – 2 km.
Câu hỏi trang 25 CH 2
|
2. Một vận động viên bơi lội người Mỹ đã từng lập kỉ lục thế giới ở nội dung bơi bướm 100 m và 200 m với thời gian lần lượt là 49,82 s và 111,51 s. Hãy lập luận để xác định vận động viên này bơi nhanh hơn trong trường hợp nào. (Nguồn số liệu: Giải vô địch các môn thể thao dưới nước thế giới năm 2009). |

Biểu thức tính tốc độ:
\(v = \frac{s}{t}\)
Trong đó:
+ s: quãng đường vật đi được (m)
+ v: tốc độ của vật (m/s)
+ t: thời gian đi được của vật (s)

Để xác định vận động ciên này bơi nhanh hơn trong trường hợp nào thì ta so sánh tốc độ trong hai trường hợp.
- Trường hợp 1: s = 100 m; t = 49,82 s
Tốc độ của vận động viên là: \(v = \frac{s}{t} = \frac{{100}}{{49,82}} \approx 2(m/s)\)
- Trường hợp 2: s = 200 m; t = 111,51 s
Tốc độ của vận động viên là: \(v = \frac{s}{t} = \frac{{200}}{{111,51}} \approx 1,79(m/s)\)
=> Tốc độ của vận động viên trong trường hợp 1 nhanh hơn trường hợp 2 nên vận động viên trong trường hợp 1 bơi nhanh hơn trường hợp 2.
Câu hỏi trang 25 CH 3
|
3. Nêu một số tình huống thực tiễn chứng tỏ tốc độ trung bình không diễn tả đúng tính nhanh chậm của chuyển động. |

Liên hệ thực tiễn

Một người đi xe máy từ nhà đến trường với tốc độ trung bình là 30 km/h. Nhưng trong quá trình di chuyển, 5 phút đầu tiên người đi xe đi với vận tốc là 50 km/h, sau đó đến đoạn đường trơn, người này giảm vận tốc xuống 25 km/h.
Từ ví dụ trên, ta thấy rằng có đoạn đường thì xe đi nhanh, có đoạn đường thì xe đi chậm
=> Tốc độ trung bình không diễn tả đúng tính nhanh chậm của chuyển động.
Câu hỏi trang 25 Luyện tập
|
Trong truyện ngụ ngôn Rùa và Thỏ, tốc độ nào cho thấy Thỏ được xem là chạy nhanh hơn Rùa? Tuy nhiên, Rùa lại chiến thắng trong cuộc đua này, hãy so sánh tốc độ trung bình của Rùa và Thỏ |

Vận dụng hiểu biết của em về câu chuyện Rùa và Thỏ, liên hệ với kiến thức bài học.

Trong truyện ngụ ngôn Rùa và Thỏ, vận tốc tức thời cho thấy Thỏ được xem là chạy nhanh hơn Rùa.
Tuy nhiên, Rùa lại chiến thắng trong cuộc đua, vì vậy tốc độ trung bình của Rùa lớn của Thỏ.
Câu hỏi trang 26 CH 4
|
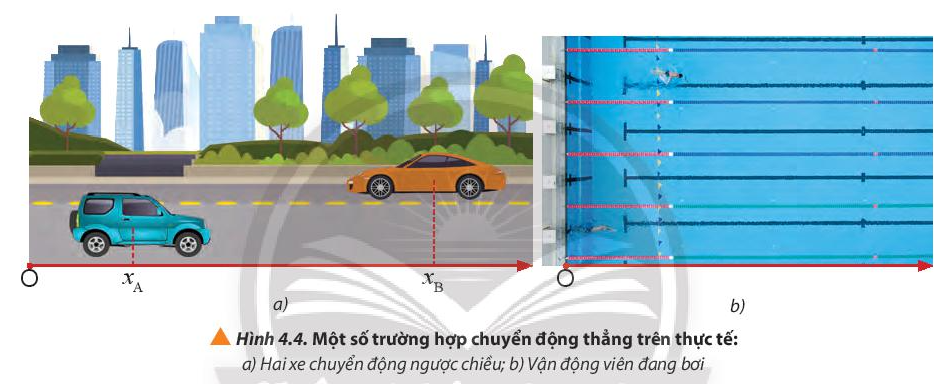
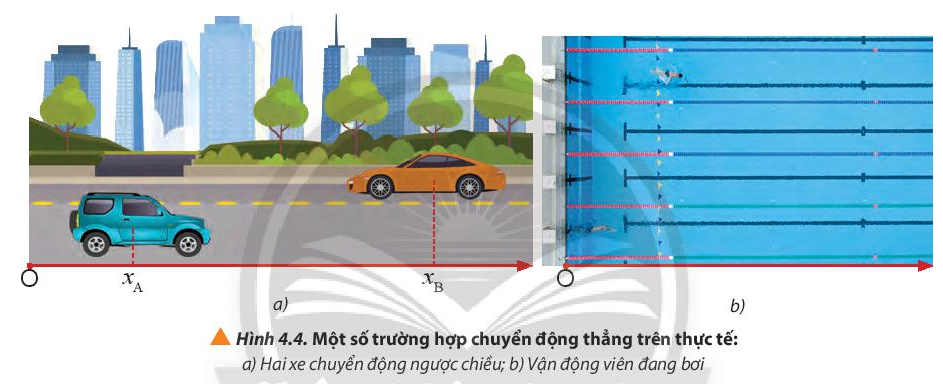
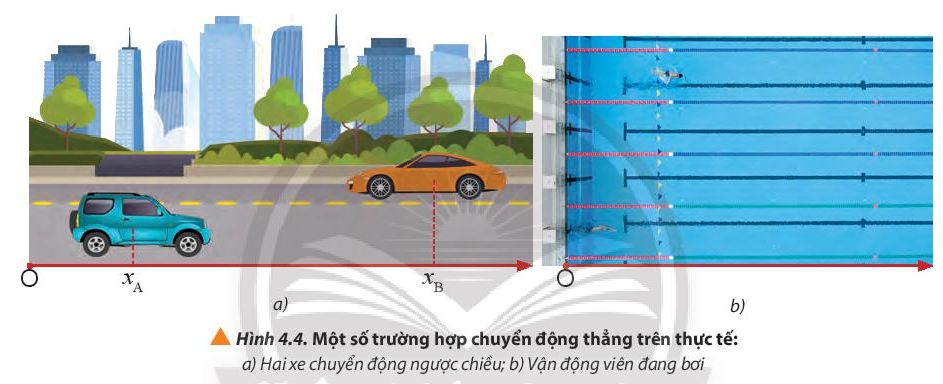
4. Quan sát hình 4.4 và đọc hai tình huống để xác định quãng đường đi được và chiều chuyển động của hai xe trong hình 4.4a và vận động viên trong hình 4.4b sau khoảng thời gian đã xác định
|

Quan sát hình vẽ

Quãng đường đi được = Khoảng cách từ vị trí đầu đến vị trí cuối trong quá trình chuyển động.
Chiều chuyển động của hai xe trong hình 4.4a:
+ Xe A chuyển động theo chiều dương
+ Xe B chuyển động ngược chiều dương
Chiều chuyển động của vận động viên bơi; Vận động viên bơi theo chiều dương.
Câu hỏi trang 26 CH 5
|
5. Xác định quãng đường đi được và độ dịch chuyển của hai xe trong tình huống 1 (Hình 4.4a) và vận động viên trong tình huống 2 (Hình 4.4b).
|

Quãng đường = Khoảng cách từ vị trí đầu đến vị trí cuối
Độ dịch chuyển = Tọa độ cuối – Tọa độ đầu.

- Tình huống 1 (Hình 4.4a)
+ Quãng đường đi được của hai xe là: sA = sB = xB – xA
+ Độ dịch chuyển của xe A: dA = xB – xA
+ Độ dịch chuyển của xe B: dB = xA – xB
- Tình huống 2 (Hình 4.4b)
+ Quãng đường và độ dịch chuyển của vận động bằng nhau và đều bằng l
Câu hỏi trang 27 Luyện tập
|
Xét quãng đường AB dài 1000 m với A là vị trí nhà của em và B là vị trí của bưu điện (Hình 4.6). Tiệm tạp hóa nằm tại vị trí C là trung điểm của AB. Nếu chọn nhà em làm gốc tọa độ và chiều dương hướng từ nhà em đến bưu điện. Hãy xác định độ dịch chuyển của em trong các trường hợp: a) Đi từ nhà đến bưu điện. b) Đi từ nhà đến bưu điện rồi quay về tiệm tạp hóa. c) Đi từ nhà đến tiệm tạp hóa rồi quay về.
|

Độ dịch chuyển = Tọa độ cuối – Tọa độ đầu.

a) Vị trí đầu: nhà, x1 = 0
Vị trí cuối: bưu điện, x2 = AB
=> Độ dịch chuyển: d = x2 – x1 = AB.
b) Vị trí đầu: nhà, x1 = 0
Vị trí cuối: tiệm tạp hóa, x2 = AC
=> Độ dịch chuyển: d = x2 – x1 = AC.
c) Vị trí đầu: nhà, x1 = 0
Vị trí cuối: nhà, x2 = 0
=> Độ dịch chuyển: d = x2 – x1 = 0.
Câu hỏi trang 27 CH 6
|
6. Xét hai xe máy cùng xuất phát tại bưu điện trong Hình 4.6 đang chuyển động thẳng với cùng tốc độ. Thảo luận để xem xét đã đủ dữ kiện để xác định vị trí của hai xe sau một khoảng thời gian xác định hay không.
|

Cách xác định vị trí:
+ Bước 1: Chọn gốc tọa độ, mốc thời gian, chọn chiều dương cho chuyển động
Advertisements (Quảng cáo)
+ Bước 2: Xác định vị trí của vật

Chưa đủ dữ kiện để xác định vị trí của hai xe, ta chưa biết là xe chuyển động theo chiều nào, có đổi chiều chuyển động hay không nên không thể xác định.
Câu hỏi trang 28 Luyện tập
|
Xác định vận tốc trung bình và tốc độ trung bình của vận động viên trong tình huống 2 ở Hình 4.4b, biết thời gian bơi của vận động viên là t.
|
Vận tốc trung bình = Quãng đường : thời gian
Tốc độ trung bình = Độ dịch chuyển : thời gian

Do vận động viên bơi không đổi chiều chuyển động nên độ dịch chuyển bằng quãng đường
=> Vận tốc trung bình = Tốc độ trung bình = l/t
Câu hỏi trang 28 CH 7
|
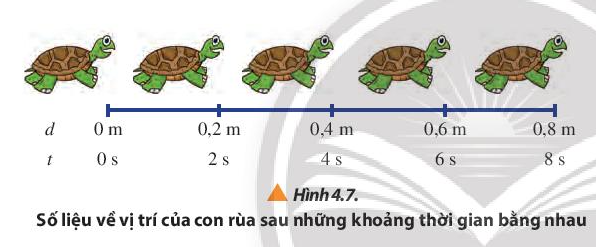
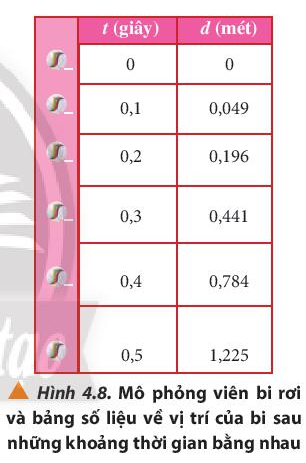
7. Dùng số liệu của hai chuyển động trong Hình 4.7 và 4.8: a) Xác định độ dịch chuyển trong các khoảng thời gian liên tiếp bằng nhau của mỗi chuyển động. b) Vẽ vào vở đồ thị dịch chuyển – thời gian (d – t) ứng với mỗi chuyển động
|

Độ dịch chuyển = Tọa độ cuối – Tọa độ đầu

a)
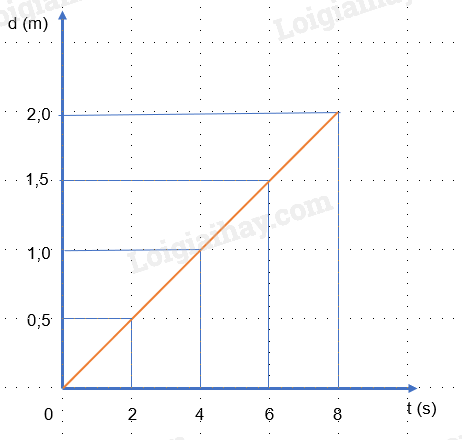
- Hình 4.7
\(\begin{array}{l}\Delta {d_1} = {x_2} - {x_1} = 0,5 - 0 = 0,5(m)\\\Delta {d_2} = {x_3} - {x_2} = 1,0 - 0,5 = 0,5(m)\\\Delta {d_3} = {x_4} - {x_3} = 1,5 - 1,0 = 0,5(m)\\\Delta {d_4} = {x_5} - {x_4} = 2,0 - 1,5 = 0,5(m)\end{array}\)
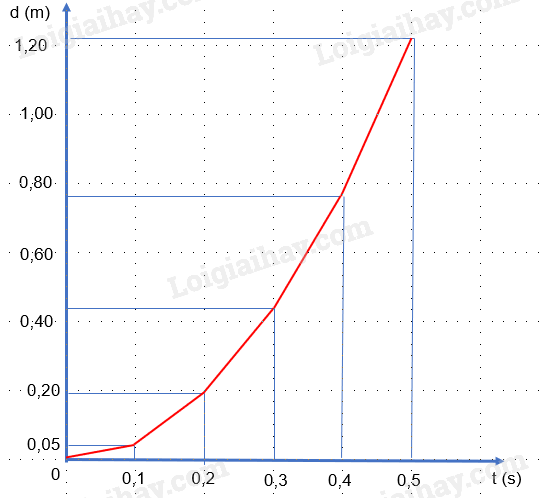
- Hình 4.8
\(\begin{array}{l}\Delta {d_1} = {x_2} - {x_1} = 0,049 - 0 = 0,049(m)\\\Delta {d_2} = {x_3} - {x_2} = 0,196 - 0,049 = 0,147(m)\\\Delta {d_3} = {x_4} - {x_3} = 0,441 - 0,196 = 0,245(m)\\\Delta {d_4} = {x_5} - {x_4} = 0,784 - 0,441 = 0,343(m)\\\Delta {d_5} = {x_6} - {x_5} = 1,225 - 0,784 = 0,441(m)\end{array}\)
b)
- Hình 4.7
- Hình 4.8
Câu hỏi trang 29
|
8. Nêu những lưu ý về dấu của độ dốc của một đường thẳng. Từ đó, hãy phân tích để suy ra được tốc độ từ độ dốc của đồ thị (d – t). |

Lưu ý về dấu của độ dốc:
+ Trong những khoảng thời gian bằng nhau, độ dịch chuyển dương thì độ dốc dương
+ Trong những khoảng thời gian bằng nhau, độ dịc chuyển âm thì độ dốc âm
=> Tốc độ = độ dốc.
Câu hỏi trang 30 Luyện tập
|
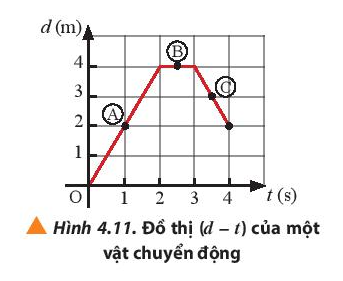
Một vật chuyển động thẳng có đồ thị (d – t) được mô tả như Hình 4.11. Hãy xác định tốc độ tức thời của vật tại các vị trí A, B và C.
|

Biểu thức tính tốc độ tức thời:
v = d/t

Tốc độ tức thời tại vị trí A: \({v_A} = \frac{{{d_A}}}{{{t_A}}} = \frac{2}{1} = 2(m/s)\)
Tốc độ tức thời tại vị trí B: \({v_B} = \frac{{{d_B}}}{{{t_B}}} = \frac{4}{{2,5}} = 1,6(m/s)\)
Tốc độ tức thời tại vị trí C: \({v_C} = \frac{{{d_C}}}{{{t_C}}} = \frac{3}{{3,5}} \approx 0,86(m/s)\)
Câu hỏi trang 30 Vận dụng
|
Một chiếc xe đồ chơi điều khiển từ xa đang chuyển động trên một đoạn đường thẳng có độ dịch chuyển tại các thời điểm khác nhau được cho trong bảng dưới đây.
a) Hãy vẽ đồ thị độ dịch chuyển – thời gian của xe đồ chơi. b) Hãy xác định vận tốc và tốc độ tức thời tại các thời điểm 2 s, 4 s, 6 s, 10 s và 16 s. |

Vận tốc tức thời = Độ dịch chuyển : Thời gian
Tốc độ tức thời = Quãng đường : Thời gian

a)
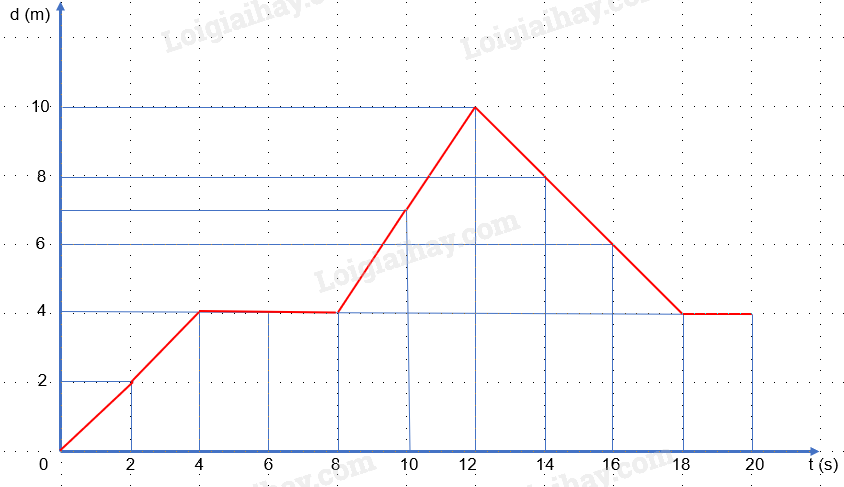
b)
- Vận tốc tức thời:
+ t = 2 s: \(v = \frac{d}{t} = \frac{2}{2} = 1(m/s)\)
+ t = 4 s: \(v = \frac{d}{t} = \frac{4}{4} = 1(m/s)\)
+ t = 6 s: \(v = \frac{d}{t} = \frac{4}{6} \approx 0,67(m/s)\)
+ t = 10 s: \(v = \frac{d}{t} = \frac{7}{{10}} = 0,7(m/s)\)
+ t = 16 s: \(v = \frac{d}{t} = \frac{6}{{16}} = 0,375(m/s)\)
- Tốc độ tức thời:
+ t = 2 s: \(v = \frac{s}{t} = \frac{2}{2} = 1(m/s)\)
+ t = 4 s: \(v = \frac{s}{t} = \frac{{2 + 4}}{4} = 1,5(m/s)\)
+ t = 6 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4}}{6} \approx 1,67(m/s)\)
+ t = 10 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4 + 4 + 7}}{{10}} = 2,1(m/s)\)
+ t = 16 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4 + 4 + 7 + 10 + 8 + 6}}{{16}} = 2,8125(m/s)\)
Câu hỏi trang 31 Bài tập 1
|
1. Hai xe chuyển động ngược chiều nhau trên cùng đoạn đường thẳng với các tốc độ không đổi. Lúc đầu, hai xe ở các vị trí A và B cách nhau 50 km và cùng xuất phát vào lúc 8 giờ 30 phút. Xe xuất phát từ A có tốc độ 60 km/h. Chọn gốc tọa độ và chiều dương tùy ý. a) Dựa vào định nghĩa của vận tốc, hãy lập hệ thức liên hệ giữa tọa độ và vận tốc của mỗi xe. Khi hai xe gặp nhau, có mối liên hệ nào giữa các tọa độ? b) Cho biết hai xe gặp nhau lúc 9 giờ. Tìm vận tốc của xe xuất phát từ B. |

a) Hệ thức liên hệ giữa tọa độ và vận tốc là: x = x0 + v.t
Với x0 là tọa độ ban đầu của vật so với gốc tọa độ; v là tốc độ của vật.
Khi hai xe gặp nhau thì tọa độ của các xe bằng nhau.
b) Chọn gốc tọa độ tại A, chiều dương từ A đến B, mốc thời gian là lúc hai xe bắt đầu xuất phát (8 giờ 30 phút).
Biểu thức tọa độ của xe A là: xA = x0A + vA .t = 0 + 60.t (km)
Biểu thức tọa độ của xe B là: xB = x0B + vB .t = 50 – vB .t (km)
Thời gian hai xe di chuyển đến lúc gặp nhau là: 9 giờ - 8 giờ 30 phút = 30 phút = 0,5 giờ
Khi hai xe gặp nhau:
\(\begin{array}{l}{x_A} = {x_B} \Leftrightarrow 60.t = 50 - {v_B}.t\\ \Leftrightarrow 60.0,5 = 50 - {v_B}.0,5\\ \Rightarrow {v_B} = 40(km/h)\end{array}\)
Câu hỏi trang 31 Bài tập 2
|
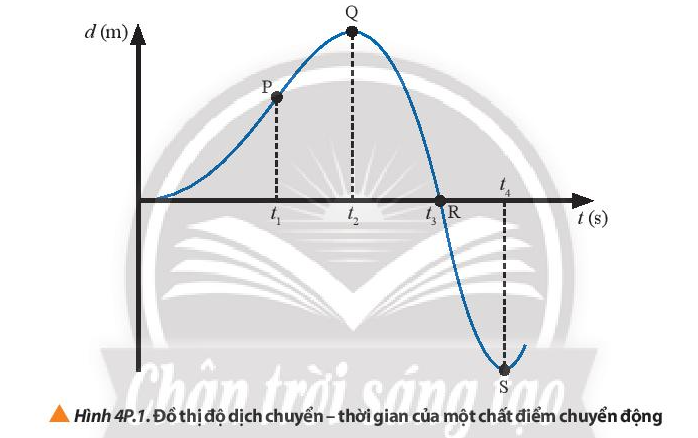
2. Hình 4P.1 là đồ thị dịch chuyển – thời gian của một chất điểm chuyển động trên đường thẳng.
Hãy sắp xếp các điểm trên đồ thị theo thứ tự: a) Vận tốc tức thời từ âm sang dương. b) Tốc độ tức thời tăng dần. |

a) Vận tốc tức thời từ âm sang dương là: S – R – Q – P.
b) Tốc độ tức thời tăng dần: R – P – S – Q.