Chứng minh hai đường thẳng vuông góc bằng cách chứng minh một đường thẳng vuông góc với một mặt phẳng chứa đường thẳng kia. Phân tích và giải - Bài 11 trang 94 sách bài tập toán 11 - Cánh diều - Bài 2. Đường thẳng vuông góc với mặt phẳng. Cho hình lăng trụ ABC. A'B'C' có \(AA' \bot \left( {ABC} \right). \)...

Cho hình lăng trụ ABC.A’B’C’ có \(AA’ \bot \left( {ABC} \right).\) Trong mặt phẳng (ABC), gọi H là hình chiếu của A trên BC. Chứng minh rằng \(BC \bot A’H.\)

Chứng minh hai đường thẳng vuông góc bằng cách chứng minh một đường thẳng vuông góc với một mặt phẳng chứa đường thẳng kia.
Advertisements (Quảng cáo)

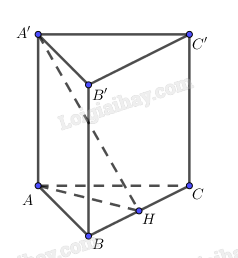
Vì \(AA’ \bot \left( {ABC} \right)\) nên \(AA’ \bot BC.\)
Mà \(BC \bot AH,{\rm{ }}AA’ \cap AH = A \Rightarrow BC \bot \left( {A’AH} \right) \Rightarrow BC \bot A’H.\)
