Sử dụng định lý ba đường vuông góc. Hướng dẫn cách giải/trả lời - Bài 14 trang 95 sách bài tập toán 11 - Cánh diều - Bài 2. Đường thẳng vuông góc với mặt phẳng. Cho hình hộp ABCD. A'B'C'D' có ABCD là hình thoi...

Cho hình hộp ABCD.A’B’C’D’ có ABCD là hình thoi, \(AA’ \bot \left( {ABCD} \right).\)Chứng minh rằng:
a) \(BB’ \bot \left( {A’B’C’D’} \right);\)
b) \(BD \bot A’C.\)

Advertisements (Quảng cáo)
Sử dụng định lý ba đường vuông góc.

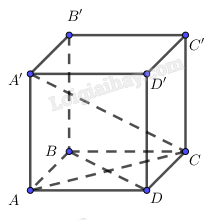
a) Vì ABCD.A’B’C’D’ là hình hộp nên \(AA'{\rm{ // }}BB’.\) Mà \(AA’ \bot \left( {ABCD} \right)\) nên \(BB’ \bot \left( {ABCD} \right).\) Mặt khác \(\left( {ABCD} \right){\rm{ // }}\left( {A’B’C’D’} \right) \Rightarrow BB’ \bot \left( {A’B’C’D’} \right).\)
b) Vì ABCD là hình thoi nên \(AC \bot BD.\) Do \(AA’ \bot \left( {ABCD} \right)\) nên AC là hình chiếu của \(A’C\) trên mặt phẳng (ABCD). Theo định lý ba đường vuông góc suy ra \(BD \bot A’C.\)
