Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước. Lời Giải - Bài 15 trang 95 sách bài tập toán 11 - Cánh diều - Bài 2. Đường thẳng vuông góc với mặt phẳng. Cho hình chóp O. ABC và điểm H không thuộc các đường thẳng AB, BC...

Cho hình chóp O.ABC và điểm H không thuộc các đường thẳng AB, BC, CA sao cho \(\widehat {OHA} = \widehat {OHB} = \widehat {OHC} = {90^0}.\)Chứng minh rằng H thuộc mặt phẳng (ABC).

Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Advertisements (Quảng cáo)
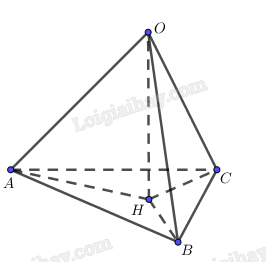
Vì H không thuộc các đường thẳng AB, BC, CA nên HA, HB, HC đôi một cắt nhau.
Theo giả thiết, \(OH \bot HA,{\rm{ }}OH \bot HB\) mà HA, HB cắt nhau nên \(OH \bot \left( {HAB} \right).\) Tương tự, \(OH \bot \left( {HBC} \right).\)Vì (HAB) và (HBC) cùng đi qua H và vuông góc với OH nên hai mặt phẳng đó trùng nhau.
Suy ra H thuộc mặt phẳng (ABC).
