Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước. Hướng dẫn giải - Bài 16 trang 95 sách bài tập toán 11 - Cánh diều - Bài 2. Đường thẳng vuông góc với mặt phẳng. Cho hình chóp S. ABC thoả mãn SA = SB = SC...
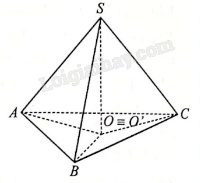
Cho hình chóp S.ABC thoả mãn SA = SB = SC. Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC. Chứng minh rằng \(SO \bot \left( {ABC} \right).\)
Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Advertisements (Quảng cáo)
Gọi \(O’\) là hình chiếu của S trên (ABC). Khi đó, \(SO’ \bot \left( {ABC} \right).\)
Mà \(O’A,{\rm{ }}O’B,{\rm{ }}O’C\) đều nằm trên (ABC) nên \(SO’ \bot O’A,{\rm{ }}SO’ \bot O’B,{\rm{ }}SO’ \bot O’C.\)
Xét ba tam giác \(SO’A,{\rm{ }}SO’B,{\rm{ }}SO’C\) vuông tại \(O’\) có SA = SB = SC và \(SO’\) chung nên ba tam giác đó bằng nhau. Do đó, \(O’A = O’B = O’C.\)
Suy ra \(O’\) là tâm đường tròn ngoại tiếp của tam giác ABC hay \(O’\) trùng O.
Vậy \(SO \bot \left( {ABC} \right).\)