
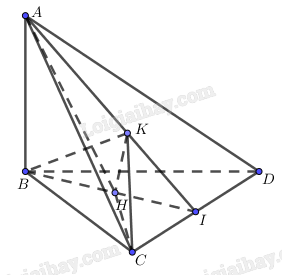
Cho hình tứ diện ABCD có \(AB \bot \left( {BCD} \right),\)các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của các tam giác BCD, ACD. Chứng minh rằng:
a) \(AD \bot CH;\)
b*) \(HK \bot \left( {ACD} \right).\)

Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.

a) Vì \(AB \bot \left( {BCD} \right),{\rm{ }}CH \subset \left( {BCD} \right) \Rightarrow AB \bot CH.\) Do H là trực tâm của tam giác (BCD) nên \(CH \bot BD.\)
Advertisements (Quảng cáo)
Mà AB, BD cắt nhau trong mặt phẳng (ABD) nên \(CH \bot \left( {ABD} \right).\)
Từ \(CH \bot \left( {ABD} \right),{\rm{ }}AD \subset \left( {ABD} \right) \Rightarrow AD \bot CH.\)
b*) Vì H là trực tâm của tam giác BCD nên \(BH \bot CD.\)
Lại có, \(AB \bot \left( {BCD} \right),{\rm{ }}CD \subset \left( {BCD} \right) \Rightarrow AB \bot CD.\)
Mà AB, BD cắt nhau trong mặt phẳng (ABI) nên \(CD \bot \left( {ABI} \right).\)
Từ \(CD \bot \left( {ABI} \right),{\rm{ }}HK \subset \left( {ABI} \right) \Rightarrow CD \bot HK.\)
Vì K là trực tâm của tam giác ACD nên \(CK \bot AD.\) Mà CK, CH cắt nhau trong mặt phẳng (CHK) nên \(AD \bot \left( {CHK} \right).\)
Lại có, \(AD \bot \left( {CHK} \right),{\rm{ }}HK \subset \left( {CHK} \right) \Rightarrow AD \bot HK.\)
Bên cạnh đó, AD, CD cắt nhau trong mặt phẳng (ACD) nên \(HK \bot \left( {ACD} \right).\)
