
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right).\) Gọi M, N, P lần lượt là trọng tâm của ba tam giác SAB, SBC, SCA. Chứng minh rằng \(SA \bot \left( {MNP} \right).\)

Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.

Advertisements (Quảng cáo)
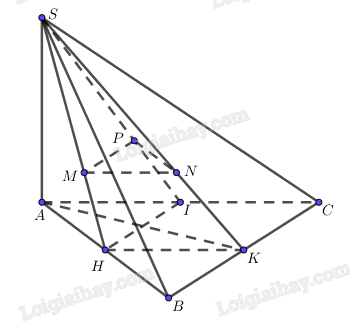
Gọi H, K, I lần lượt là trung điểm của AB, BC, CA.
Theo giả thiết ta có: \(\frac{{SM}}{{SH}} = \frac{{SN}}{{SK}} = \frac{{SP}}{{SI}} = \frac{2}{3}.\)
Theo định lý Ta-lét: Trong tam giác SHK có \(MN{\rm{ // }}HK,\) trong tam giác SHI có \(MP{\rm{ // }}HI.\) Mà \(HK \subset \left( {ABC} \right),{\rm{ }}HI \subset \left( {ABC} \right)\) nên \(MN{\rm{ // }}\left( {ABC} \right),{\rm{ }}MP{\rm{ // }}\left( {ABC} \right).\)Mà, MN, MP cắt nhau trong mặt phẳng (MNP) nên \(\left( {MNP} \right){\rm{ // }}\left( {ABC} \right).\)
Ta lại có, \(SA \bot \left( {ABC} \right).\) Vậy \(SA \bot \left( {MNP} \right).\)
