Dựa vào kiến thức hai đường thẳng vuông góc và các cách xác định góc giữa hai đường thẳng đã học để làm. Hướng dẫn giải - Bài 3 trang 89 sách bài tập toán 11 - Cánh diều - Bài 1. Hai đường thẳng vuông góc. Cho hình hộp \(ABCD. A'B'C'D'\) có đáy là hình vuông...

Cho hình hộp \(ABCD.A’B’C’D’\) có đáy là hình vuông.
a) Chứng minh rằng \(AB \bot A’D’\)và \(AC \bot B’D’.\)
b) Tính góc giữa hai đường thẳng \(AC\) và \(A’B’.\)

Dựa vào kiến thức hai đường thẳng vuông góc và các cách xác định góc giữa hai đường thẳng đã học để làm.

Advertisements (Quảng cáo)
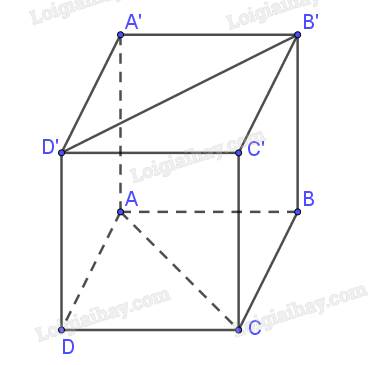
a) Do \(A’B’C’D’\) là hình vuông nên \(A’D’ \bot A’B’,A’C’ \bot B’D’.\)
Ta có: \(AB\)// \(A’B’ \Rightarrow \)\(AB \bot A’D’.\)
\(AC\)// \(A’C’ \Rightarrow \)\(AC \bot B’D’.\)
b) Do \(ABCD\) là hình vuông nên \(\widehat {CAB} = \frac{1}{2}\widehat {DAB} = \frac{1}{2}{.90^0} = {45^0}.\)
Ta có: \(AB\)// \(A’B’\) nên \(\left( {AC,A’B’} \right) = \left( {AC,AB} \right) = \widehat {CAB} = {45^0}.\)
