
Cho hình chữ nhật \(ABCD\) có \(AB = 3a\), \(AD = 4a\).
a) Khoảng cách từ điểm \(A\) đến đường thẳng \(BC\) bằng:
A. \(2,4a\)
B. \(3a\)
C. \(4a\)
D. \(5a\)
b) Khoảng cách từ điểm \(A\) đến đường thẳng \(BD\) bằng:
A. \(2,4a\)
B. \(3a\)
C. \(4a\)
D. \(5a\)
c) Khoảng cách giữa hai đường thẳng \(AB\) và \(CD\) bằng:
A. \(2,4a\)
Advertisements (Quảng cáo)
B. \(3a\)
C. \(4a\)
D. \(5a\)

Khoảng cách từ 1 điểm đến 1 đường thẳng là độ dài đoạn thẳng nối điểm đó và hình chiếu của nó trên đường thẳng.
Khoảng cách giữa 2 đường thẳng song song là khoảng cách từ 1 điểm của đường thẳng này đến đường thẳng kia.

a) Do \(ABCD\) là hình chữ nhật, nên ta có \(AB \bot BC\). Như vậy khoảng cách từ điểm \(A\) đến đường thẳng \(BC\) là đoạn thẳng \(AB\). Do \(AB = 3a\), nên đáp án cần chọn là đáp án B.
b) Gọi \(H\) là hình chiếu của \(A\) trên \(BD\). Khi đó khoảng cách từ \(A\) đến \(BD\) là đoạn thẳng \(AH\).
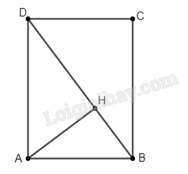
Tam giác \(ABD\) vuông tại \(A\), đường cao \(AH\) nên ta có \(BD = \sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}} = 5a\)
Như vậy \(AH = \frac{{AB.AD}}{{BD}} = \frac{{3a.4a}}{{5a}} = 2,4a\).
Đáp án cần chọn là đáp án A.
c) Do \(AB\parallel CD\) nên khoảng cách giữa 2 đường thẳng này chính là khoảng cách từ điểm \(A\) đến đường thẳng \(CD\). Vì \(AD \bot DC\) nên khoảng cách giữa hai đường thẳng \(AB\) và \(CD\) chính là đoạn thẳng \(AD\). Mà \(AD = 4a\), nên đáp án đúng là đáp án C.
