
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Trên cạnh \(SA\) lấy điểm \(M\) sao cho \(MA = 2MS\). Mặt phẳng \(\left( {CDM} \right)\) cắt \(SB\) tại \(N\). Tỉ số \(\frac{{SN}}{{SB}}\) bằng:
A. \(\frac{1}{2}\)
B. \(\frac{1}{3}\)
C. \(\frac{2}{3}\)
D. \(\frac{3}{4}\)

Advertisements (Quảng cáo)
Chứng minh rằng \(MN\) là giao tuyến của hai mặt phẳng \(\left( {CDM} \right)\) và \(\left( {SAB} \right)\), từ đó suy ra \(MN\parallel AB\) và tính tỉ số \(\frac{{SN}}{{SB}}\).

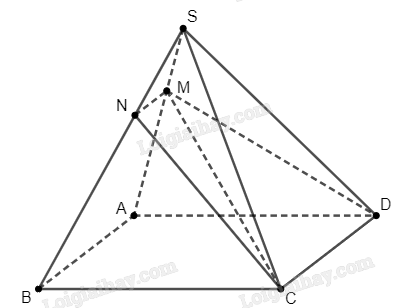
Ta thấy rằng \(M \in \left( {CDM} \right) \cap \left( {SAB} \right)\) và \(N\) là giao điểm của \(\left( {CDM} \right)\) và \(SB\). Do \(SB \subset \left( {SAB} \right)\) nên \(N\) là điểm chung của hai mặt phẳng \(\left( {CDM} \right)\) và \(\left( {SAB} \right)\). Từ đó ta suy ra \(MN\) là giao tuyến của hai mặt phẳng \(\left( {CDM} \right)\) và \(\left( {SAB} \right)\).
Nhận xét rằng \(AB\parallel CD\), \(AB \subset \left( {SAB} \right)\), \(CD \subset \left( {CDM} \right)\), \(MN\) là giao tuyến của hai mặt phẳng \(\left( {CDM} \right)\) và \(\left( {SAB} \right)\), ta suy ra \(MN\parallel AB\).
Theo định lý Thales, ta có \(\frac{{SM}}{{SA}} = \frac{{SN}}{{SB}}\). Do \(MA = 2MS \Rightarrow \frac{{SM}}{{SA}} = \frac{1}{3}\).
Như vậy \(\frac{{SN}}{{SB}} = \frac{1}{3}\). Đáp án đúng là B.
