Câu hỏi/bài tập:
12.1
Đề bài:
Hình 12.1 mô tả đường sức điện của các điện tích. Hãy xác định dấu của các điện tích trong từng trường hợp.

Phương pháp giải
Dựa vào chiều đường sức điện

Hình a: q1>0, q2<0; Hình b: q1>0,q2>0; Hình c: q < 0 .
12.2
Đề bài:
Có thể dùng điện tích thử âm để khảo sát cường độ điện trường do điện tích điểm gây ra được không? Giải thích.
Phương pháp giải
Dựa vào mối quan hệ giữa điện tích thử và cường độ điện trường

Vì cường độ điện trường do một điện tích điểm gây ra trong không gian không phụ thuộc vào điện tích thử nên ta có thể dùng điện tích thử âm. Khi đó, chiều của lực điện tác dụng lên điện tích thử ngược chiều với chiều vectơ cường độ điện trường.
12.3
Đề bài:
Đặt một điện tích -3.10-6 C tại điểm A trong chân không. Xác định cường độ điện trường tại B, biết AB = 15 cm
Phương pháp giải
Áp dụng công thức tính cường độ điện trường

Độ lớn cường độ điện trường tại B: \(E = \frac{{k\left| Q \right|}}{{{r^2}}} = \frac{{{{9.10}^9}.\left| { - {{3.10}^{ - 6}}} \right|}}{{0,{{15}^2}}} = {12.10^5}V/m\), hướng từ B về A
12.4
Đề bài:
Một điện tích Q đặt trong chân không, cường độ điện trường tại điểm M cách Q là 20 cm, có độ lớn 450 V/m. Tính độ lớn của điện tích Q.
Phương pháp giải
Áp dụng công thức tính cường độ điện trường

Độ lớn của điện tích: \(\left| Q \right| = \frac{{E{r^2}}}{k} = \frac{{450.0,{2^2}}}{{{{9.10}^9}}} = {2.10^{ - 9}}C\)
12.5
Đề bài:
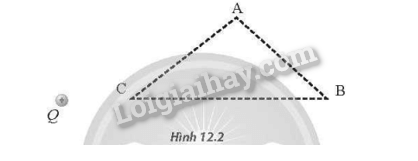
Sắp xếp độ lớn cường độ điện trường do điện tích điểm Q gây ra tại các điểm A, B, C (Hình 12.2) theo thứ tự tăng dần.
Phương pháp giải
Xác định cường độ điện trường tại các điểm

Cường độ điện trường tỉ lệ nghịch với bình phương khoảng cách từ điểm đó đến điện tích nên EB<EA<EC
12.6
Đề bài:
Hai điện tích điểm có giá trị điện tích lần lượt là +3,0μC và −5,0μC được đặt tại hai điểm M và N trong chân không. Khoảng cách giữa M và N là 0,2 m. Gọi P là điểm mà cường độ điện trường tổng hợp tại đó bằng 0. Hãy xác định vị trí điểm P.
Phương pháp giải
Áp dụng công thức tính cường độ điện trường

Do hai điện tích tại M và N trái dấu nên điểm P nằm ngoài đoạn MN và gần M hơn (do độ lớn điện tích tại M nhỏ hơn độ lớn điện tích tại N).

Ta có \(\left| {{E_1}} \right| = \left| {{E_2}} \right| \Rightarrow \frac{{k\left| {{q_1}} \right|}}{{M{P^2}}} = \frac{{k\left| {{q_2}} \right|}}{{{{(MP + 0,2)}^2}}} \Rightarrow \frac{3}{{M{P^2}}} = \frac{5}{{{{(MP + 0,2)}^2}}} \Rightarrow \left\{ \begin{array}{l}MP \approx 0,69m\\NP \approx 0,89m\end{array} \right.\)
12.7
Đề bài:
Một electron tự do có điện tích và khối lượng lần lượt là −1,6.10−19C và 9,1.10−31 kg được đặt vào điện trường đều E = 300 V/m. Tính độ lớn gia tốc mà electron thu được dưới tác dụng của lực tĩnh điện.
Advertisements (Quảng cáo)
Phương pháp giải
Áp dụng công thức tính lực điện và định luật 2 Newton

Ta có: \(F = \left| q \right|E = ma\)
Độ lớn gia tốc mà electron thu được dưới tác dụng của lực tĩnh điện là:
\(a = \frac{{\left| q \right|E}}{m} = \frac{{\left| { - 1,{{6.10}^{ - 19}}} \right|.300}}{{9,{{1.10}^{ - 31}}}} \approx 5,{3.10^{13}}m/{s^2}\)
12.8
Đề bài:
Đặt một điện tích Q=10−6Cvào một môi trường có hằng số điện môi bằng 3.
a) Xác định vectơ cường độ điện trường tại điểm M cách Q là 2 cm.
b) Đặt tại M một điện tích q=−2.10−8C. Xác định lực điện tác dụng lên q.
Phương pháp giải
Áp dụng công thức tính cường độ điện trường

a) Độ lớn cường độ điện trường tại M: \(E = \frac{{k\left| Q \right|}}{{\varepsilon {r^2}}} = \frac{{{{9.10}^9}.\left| {{{10}^{ - 6}}} \right|}}{{3.0,{{02}^2}}} = 7,{5.10^6}V/m\)
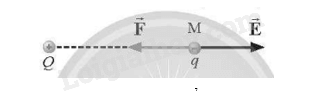
Hướng như hình vẽ:

b) Độ lớn lực điện tác dụng lên q: \(F = \left| q \right|E = \left| { - {{2.10}^{ - 8}}} \right|.7,{5.10^6} = 0,15N\)
Hướng như hình vẽ:
12.9
Đề bài:
Cho hai điểm M và N cùng nằm trên một đường sức điện của điện trường do điện tích q gây ra. Độ lớn cường độ điện trường tại M là 45 V/m và tại N là 5 V/m. Độ lớn cường độ điện trường tại trung điểm I bằng bao nhiêu?
Phương pháp giải
Áp dụng công thức tính cường độ điện trường

Gọi O là điểm ta đặt điện tích q, áp dụng các công thức tính cường độ điện trường tại M, N ta có: \(\left\{ \begin{array}{l}{E_M} = k\frac{{\left| q \right|}}{{O{M^2}}}\\{E_N} = k\frac{{\left| q \right|}}{{O{N^2}}}\end{array} \right. \Rightarrow \frac{{{E_M}}}{{{E_N}}} = \frac{{O{N^2}}}{{O{M^2}}} = \frac{{45}}{5} = 9 \Rightarrow ON = 3OM\)
Ta có: \(\left\{ \begin{array}{l}OI = OM + \frac{{MN}}{2}\\MN = OI - OM = 2OM\end{array} \right. \Rightarrow OI = 2OM\)
Độ lớn cường độ điện trường tại I: \({E_1} = k\frac{q}{{O{I^2}}} = k\frac{q}{{4O{M^2}}} = \frac{1}{4}{E_M} = \frac{1}{4}.45 = 11,25V/m\)
12.10
Đề bài:
Có thể xem mô hình hạt nhân uranium là một quả cầu có bán kính 7,40.10-15 m. Biết hạt nhân uranium có 92 proton, điện tích của một hạt proton là 1,60.10-19 C. Xem gần đúng toàn bộ điện tích của hạt nhân uranium tập trung tại tâm của quả cầu. Hạt nhân uranium sau đó giải phóng một hạt α chứa 2 proton tại bề mặt của hạt nhân (hiện tượng phóng xạ).
a) Tính cường độ điện trường tại bề mặt hạt nhân trước khi giải phóng hạt α
b) Tính lực điện tác dụng lên hạt α tại bề mặt hạt nhân.
Phương pháp giải
Áp dụng công thức tính cường độ điện trường

a) Cường độ điện trường trước khi phóng xạ: \(E = \frac{{k\left| q \right|}}{{{r^2}}} = \frac{{{{9.10}^9}.\left| {92.1,{{6.10}^{ - 19}}} \right|}}{{{{(7,{{4.10}^{ - 15}})}^2}}} \approx 2,{42.10^{21}}V/m\)
b) Cường độ điện trường sau khi phóng xạ: \(E’ = \frac{{k\left| {q’} \right|}}{{{r^2}}} = \frac{{{{9.10}^9}.\left| {(92 - 2).1,{{6.10}^{ - 19}}} \right|}}{{{{(7,{{4.10}^{ - 15}})}^2}}} \approx 2,{37.10^{21}}V/m\)
Lực điện tác dụng lên hạt α: \(F = {q_\alpha }E’ \approx 2.1,{60.10^{ - 19}}.2,{37.10^{21}} \approx 758{\rm{N}}\)
12.11
Đề bài:
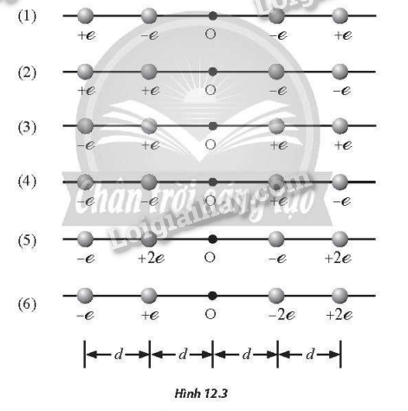
Hình 12.3 mô tả 6 trường hợp sắp xếp 4 điện tích điểm, trong đó các điện tích được đặt cách đều nhau bên trái và bên phải so với điểm O. Hãy sắp xếp độ lớn cường độ điện trường tại điểm O theo thứ tự tăng dần.
Phương pháp giải
Tổng hợp cường độ điện trường

(1)<(3)<(4)<(5)=(6)<(2)
Độ lớn cường độ điện trường tại điểm O trong các trường hợp:\({E_1} = 0,{E_2} = 2,5\frac{{ke}}{{{d^2}}},{E_3} = 0,5\frac{{ke}}{{{d^2}}},{E_4} = 2\frac{{ke}}{{{d^2}}},{E_5} = {E_6} = 2,25\frac{{ke}}{{{d^2}}}\)
