Tự luận trang 60, 61, 62 SBT Vật lý 11 - Chân trời sáng tạo: Dòng điện không đổi chạy trong một dây dẫn, cứ mỗi giây có 1,6 C chuyển qua tiết diện thẳng của dây dẫn...

16.1

Đề bài:

Dòng điện không đổi chạy trong một dây dẫn, cứ mỗi giây có 1,6 C chuyển qua tiết diện thẳng của dây dẫn. Tính cường độ dòng điện.

Phương pháp giải

Áp dụng công thức tính cường độ dòng điện

Cường độ dòng điện là:\(I = \frac{{{\rm{\Delta }}q}}{{{\rm{\Delta }}t}} = \frac{{1,6}}{1} = 1,6{\rm{\;A}}\)

16.2

Đề bài:

Dòng điện không đồi có cường độ 1,5 A chạy trong dây dẫn kim loại.

a) Tính điện lượng chuyển qua tiết diện thẳng của dây trong 1 s.

b) Tính số electron chuyển qua tiết diện thẳng của dây trong 1 s.

Phương pháp giải

Vận dụng công thức tính điện lượng và số hạt

a) Điện lượng chuyển qua tiết diện thẳng của dây trong: \({\rm{\Delta }}q = I{\rm{\Delta }}t = 1,5.1 = 1,5{\rm{C}}\)

b) Số electron chuyển qua tiết diện thẳng của dây trong: \(N = \frac{{{\rm{\Delta }}q}}{e} = \frac{{1,5}}{{1,{{6.10}^{ - 19}}}} = 9,{375.10^{18}}{\rm{\;electron\;}}\)

16.3

Đề bài:

Dòng điện không đổi có cường độ 2,8 A chạy trong một dây dẫn kim loại có diện tích tiết diện thẳng 3,2.10^-6 m². Biết mật độ electron trong dây dẫn là 8,5.10²⁸ electron/m³. Tính vận tốc trôi của electron.

Phương pháp giải

Vận dụng công thức tính vận tốc trôi

Vận tốc trôi của electron: \(v = \frac{I}{{{\rm{\;Sne\;}}}} = \frac{{2,8}}{{3,{{2.10}^{ - 6}}.8,{{5.10}^{28}}.1,{{6.10}^{ - 19}}}} \approx 0,{064.10^{ - 3}}{\rm{\;m}}/{\rm{s}}\)

16.4

Đề bài:

Hai dây dẫn (1) và (2) được làm từ cùng một loại vật liệu kim loại, có cùng một cường độ dòng điện chạy qua nhưng bán kính dây (1) lớn gấp 3 lần bán kính dây (2). Tính tỉ số tốc độ trôi của electron dẫn trong hai dây dẫn đang xét.

Phương pháp giải

Vận dụng công thức tính vận tốc trôi

Tỉ số tốc độ trôi của electron dẫn trong hai dây dẫn đang xét: \(I = {S_1}ne{v_1} = {S_2}ne{v_2} \Rightarrow \frac{{{v_1}}}{{{v_2}}} = \frac{{{S_2}}}{{{S_1}}} = \frac{{\pi r_2^2}}{{\pi r_1^2}} = \frac{{r_2^2}}{{r_1^2}} = \frac{{r_2^2}}{{{{\left( {3{r_2}} \right)}^2}}} = \frac{1}{9}\)

16.5

Đề bài:

Hai dòng điện không đổi (1) và (2) có đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện theo thời gian như Hình 16.2.

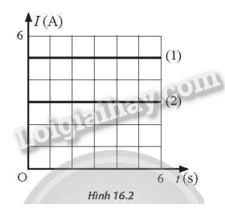
a) Hãy tính điện lượng do dòng điện (1) đi qua tiết diện thẳng của dây trong khoảng thời gian từ t₁=2 s đến t₂=4 s

b) Hãy tính điện lượng do dòng điện (2) đi qua tiết diện thẳng của dây trong khoảng thời gian từ t₃=3 s đến t₄=6 s.

Phương pháp giải

Vận dụng công thức tính điện lượng

a) Điện lượng do dòng điện (1) đi qua tiết diện thẳng của dây trong khoảng thời gian từ \({t_1} = 2s\)đến \({t_2} = 4s\): \({\rm{\Delta }}{q_1} = {I_1}\left( {{t_2} - {t_1}} \right) = 5.\left( {4 - 2} \right) = 10{\rm{C}}\)

b) Điện lượng do dòng điện (2) đi qua tiết diện thẳng của dây trong khoảng thời gian từ \({t_1} = 3{\rm{s}}\) đến \({t_2} = 6s\):\({\rm{\Delta }}{q_2} = {I_2}\left( {{t_4} - {t_3}} \right) = 3.\left( {6 - 3} \right) = 9{\rm{C}}\)

16.6

Đề bài:

Một lượng kim loại được nấu nóng chảy và kéo thành một đoạn dây dẫn. Cho dòng điện I chạy qua đoạn dây đó thì thời gian trung bình một electron đi từ đầu đến cuối đoạn dây là 4 giờ 30 phút. Nếu đoạn dây đó được nấu nóng chảy rồi kéo thành đoạn dây có chiều dài gấp đôi chiều dài ban đầu, sau đó vẫn cho dòng điện I như trên chạy qua thì thời gian trung bình một electron đi từ đầu đến cuối đoạn dây bằng bao nhiêu?

Phương pháp giải

Áp dụng công thức tính vận tốc trôi

Áp dụng: \(I = {S_1}ne{v_1} = {S_2}ne{v_2} \Rightarrow {S_1}{v_1} = {S_2}{v_2} \Rightarrow {S_1}\frac{{{\ell _1}}}{{{t_1}}} = {S_2}\frac{{{\ell _2}}}{{{t_2}}}\)

Vì cùng một lượng kim loại nên: \({S_1}{\ell _1} = {S_2}{\ell _2} \Rightarrow {t_1} = {t_2} = 4,5h\)

Vậy thời gian trung bình một electron đi từ đầu đến cuối đoạn dây vẫn không đổi và bằng 4 giờ 30 phút.

16.7

Đề bài:

Coi Trái Đất là một quả cầu bán kính 6400 km. Giả sử có một lượng điện tích tương ứng với dòng điện 1,0 A chuyển qua một tiết diện thẳng của vật dẫn trong 1 giờ được phân bố đều trên bề mặt thì mật độ điện tích trên bề mặt Trái Đất bằng bao nhiêu C/m²?

Phương pháp giải

Vận dụng công thức tính mật độ điện tích

Điện lượng: q=It=1,0.3600=3600C

Diện tích bề mặt Trái Đất: S=4πr²=4π(6400000)²=5,147.10¹⁴ m²

Mật độ điện tích trên bề mặt Trái Đất mặt: \(\sigma = \frac{q}{S} = \frac{{3600}}{{5,{{147.10}^{14}}}} \approx {7.10^{ - 12}}{\rm{C}}/{{\rm{m}}^2}\)

16.8

Đề bài:

Nhôm là loại vật liệu có khối lượng riêng 2,7 tấn/m³ và khối lượng mol nguyên tử là 27 g/mol. Biết rằng mỗi nguyên tử nhôm có tương ứng 3 electron tự do. Một dây dẫn bằng nhôm có đường kính tiết diện 3,0 mm mang dòng điện 15 A. Tính tốc độ trôi của electron trong dây dẫn bằng nhôm này.

Phương pháp giải

Vận dụng công thức tính vận tốc trôi

Mật độ nguyên tử nhôm, với D là khối lượng riêng, A là số khối:\(n = 3\frac{N}{V} = 3\frac{m}{A} \cdot \frac{{{N_{\rm{A}}}}}{V} = 3\frac{{D{N_{\rm{A}}}}}{A}\)

Thay vào:

\(\begin{array}{l}v = \frac{I}{{{\rm{\;Sne\;}}}} = \frac{{4IA}}{{3\pi {d^2}e{N_{\rm{A}}}D}}\\\; = \frac{{{{4.15.27.10}^{ - 3}}}}{{3\pi {{\left( {3,{{0.10}^{ - 3}}} \right)}^2}.1,{{6.10}^{ - 19}}.6,{{022.10}^{23}}.2700}} = 0,{073.10^{ - 3}}{\rm{\;m/s}} = 0,073{\rm{\;mm/s}}\end{array}\)