Tự luận trang 63, 64, 65, 66, 67 SBT Vật lý 11 - Chân trời sáng tạo: Một đoạn dây dẫn bằng đồng có điện trở suất 1, 69. 10−8Ωm, dài 2,0 m và đường kính tiết diện là 1,0 mm...

17.1

Đề bài:

Một đoạn dây dẫn bằng đồng có điện trở suất 1,69.10⁻⁸Ωm, dài 2,0 m và đường kính tiết diện là 1,0 mm. Cho dòng điện 1,5 A chạy qua đoạn dây.

a) Tính điện trở của đoạn dây.

b) Tính hiệu điện thế giữa hai đầu đoạn dây.

Phương pháp giải

Áp dụng công thức tính điện trở

a) Điện trở của đoạn dây: \(R = \rho \frac{\ell }{S} = \rho \frac{{4\ell }}{{\pi {d^2}}} = 1,{69.10^{ - 8}}.\frac{{4.2}}{{\pi {{\left( {0,001} \right)}^2}}} \approx 0,043{\rm{\Omega }}\)

b) Hiệu điện thế giữa hai đầu đoạn dây: \(U = RI = 0,043.1,5 = 0,065{\rm{\;V}}\)

17.2

Đề bài:

Với 2 điện trở 3Ω và 6Ω mắc thành bộ rồi đặt hiệu điện thế U vào hai đầu bộ điện trở. Xét hai trường hợp:

a) Hai điện trở mắc nối tiếp. Tính U sao cho hiệu điện thế giữa hai đầu điện trở 6Ω bằng 4 V.

b) Hai điện trở mắc song song. Tính U sao cho cường độ dòng điện qua điện trở 3Ω là 0,5 A.

Phương pháp giải

Vận dụng công thức mắc điện trở nối tiếp, song song

a) Khi mắc nối tiếp thì cường độ dòng điện qua hai điện trở bằng nhau:

\(U = {U_1} + {U_2} = 4 + 3.\frac{4}{6} = 4 + 2 = 6\;V\)

b) Khi mắc song song thì hiệu điện thế trên hai điện trở bằng nhau:

\(U = 3.0,5 = 1,5{\rm{\;V}}\)

17.3

Đề bài:

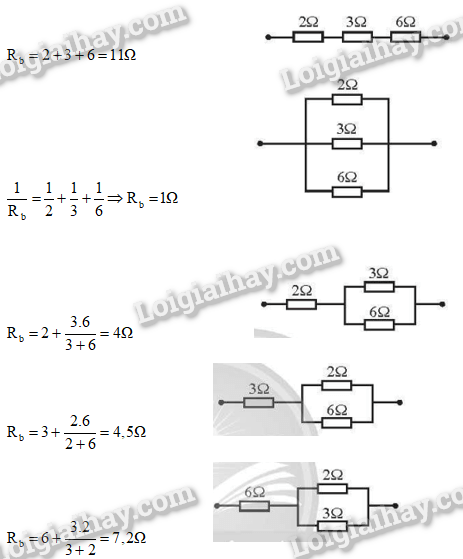
Có 3 điện trở 2Ω;3Ω;6Ω ghép thành bộ. Tìm tất cả các giá trị có thể có của bộ 3 điện trở này.

Phương pháp giải

Vận dụng công thức mắc điện trở nối tiếp, song song

Có 5 giá trị từ nhỏ đến lớn: 1Ω;4Ω;4,5Ω;7,2Ω;11Ω

17.4

Đề bài:

Có 3 điện trở giống nhau được ghép thành bộ theo tât cả các cách và hai đầu bộ điện trở được đặt vào một hiệu điện thế không đổi. Đo cường độ dòng điện chạy qua mạch chính của bộ điện trở, kết quả cho thấy trường hợp cường độ dòng điện có giá trị nhỏ nhất là 0,3 A.

a) Có bao nhiêu giá trị khác nhau của cường độ dòng điện trên?

b) Tính các giá trị cường độ dòng điện trong các trường hợp còn lại.

Phương pháp giải

Vận dụng công thức mắc điện trở nối tiếp, song song

a) Với 3 điện trở giống nhau bằng R thì có tất cả 3 cách ghép khác nhau. Do đó, có 3 giá trị khác nhau của cường độ dòng điện.

b) Trường hợp cường độ dòng điện nhỏ nhất ứng với điện trở của bộ lớn nhất: \({R_{\rm{b}}} = 3R \Rightarrow {I_{{\rm{min}}}} = \frac{U}{{3R}} = 0,3{\rm{\;A}}\)

Trường hợp cường độ dòng điện lớn nhất ứng với điện trở của bộ nhỏ nhất: \({R_{\rm{b}}} = \frac{R}{3} \Rightarrow {I_{{\rm{max}}}} = \frac{{3U}}{R} = \frac{{9U}}{{3R}} = 9.0,3 = 2,7{\rm{\;A}}\)

Trường hợp còn lại: \({R_{\rm{b}}} = \frac{{3R}}{2} \Rightarrow I = \frac{{2U}}{{3R}} = 2.0,3 = 0,6{\rm{\;A}}\)

17.5

Đề bài:

Đặt một hiệu điện thế không đổi vào hai đầu đoạn dây kim loại đồng chất có tiết diện đều thì khoảng thời gian trung bình một hạt tải điện đi hết chiều dài đoạn dây là 5,0 phút. Nếu tăng chiều dài đoạn dây lên gấp 3 lần thì thời gian trung bình mà hạt tải điện đi bằng bao nhiêu?

Phương pháp giải

Áp dụng công thức tính vận tốc trôi và định luật Ohm

Áp dụng công thức \(I = Snev = {\rm{Sn}}e.\frac{\ell }{t}\) và định luật Ohm:\(I = \frac{U}{R} = \frac{{US}}{{\rho \ell }}\)\( \Rightarrow t = \frac{{ne\rho {\ell ^2}}}{U}\)

Vậy thời gian trung bình mà hạt tải điện di chuyển tăng tỉ lệ với bình phương chiều dài đoạn dây.

Khi tăng chiều dài đoạn dây lên gấp 3 lần thì thời gian trung bình mà hạt tải điện đi là: \(t = {5.3^2} = 45\)phút

17.6

Đề bài:

Với cùng một khối lượng đồng nguyên chất như nhau, người ta tạo thành hai đoạn dây dẫn hình trụ (1) và (2). Biết đường kính tiết diện của dây (1) bằng một nửa so với dây (2). Tính tỉ số điện trở của hai đoạn dây dẫn (1) và (2).

Phương pháp giải

Vận dụng công thức tính điện trở

Với m, D, ρ lần lượt là khối lượng, khối lượng riêng và điện trở suất của đồng. Ta có: \(\left\{ {\begin{array}{*{20}{l}}{m = DV = D\ell S}\\{R = \rho \frac{\ell }{S}}\end{array} \Rightarrow R = \frac{{\rho m}}{{D{S^2}}} = \frac{{16\rho m}}{{D{\pi ^2}{{\rm{d}}^4}}}} \right.\) Như vậy, điện trở đoạn dây tỉ lệ nghịch với lũy thừa bậc 4 của đường kính tiết diện dây. Do đó, điện trở dây (1) lớn gấp 2⁴=16 lần so với điện trở dây (2).

17.7

Đề bài:

Biết bạc có khối lượng riêng và điện trở suất lần lượt là 10,5 tấn/m³; 1,62.10⁻⁸Ωm; nhôm có khối lượng riêng và điện trở suất lần lượt là 2,7 tấn/m³; 2,75.10⁻⁸Ωm. Xét hai dây dẫn có cùng tiết diện và cùng điện trở, một dây làm bằng bạc và một dây làm bằng nhôm. Nếu dây bằng nhôm có khối lượng 200 kg thì dây bằng bạc có khối lượng bao nhiêu?

Phương pháp giải

Vận dụng công thức tính điện trở

Gọi bạc là (1), nhôm là (2).

Theo đề, ta có: \({R_1} = {R_2} \Rightarrow {\rho _1}\frac{{{\ell _1}}}{{{S_1}}} = {\rho _2}\frac{{{\ell _2}}}{{{S_2}}} \Rightarrow {\rho _1}{\ell _1} = {\rho _2}{\ell _2} \Rightarrow \frac{{{\ell _1}}}{{{\ell _2}}} = \frac{{{\rho _2}}}{{{\rho _1}}}\left( {{\rm{do\;}}{S_1} = {S_2}} \right)(1)\)

Tỉ số khối lượng: \(\frac{{{m_1}}}{{{m_2}}} = \frac{{{D_1}{V_1}}}{{{D_2}{V_2}}} = \frac{{{D_1}{S_1}{\ell _1}}}{{{D_2}{S_2}{\ell _2}}} = \frac{{{D_1}{\ell _1}}}{{{D_2}{\ell _2}}}(2)\)

Thế (1) vào (2), ta được: \(\frac{{{m_1}}}{{{m_2}}} = \frac{{{D_1}{\rho _2}}}{{{D_2}{\rho _1}}} = \frac{{10,5.2,{{75.10}^{ - 8}}}}{{2,7.1,{{62.10}^{ - 8}}}} \approx 6,6 \Rightarrow {m_1} = 6,6{m_2} = 6,6.200 = 1320{\rm{\;kg}}\)

17.8

Đề bài:

Tính giá trị điện trở R ở Hình 17.2. Bỏ qua điện trở các dây nối. Biết điện trở tương đương giữa hai điểm A và B có giá trị 3Ω

Phương pháp giải

Vẽ lại mạch điện bằng cách chập điểm có cùng điện thế

Đặt tên các điểm nút được nối với nhau bằng đoạn dây không điện trở như hình dưới.

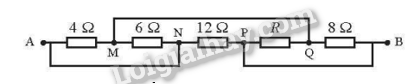
Sau đó, vẽ lại mạch với các cặp điểm trùng nhau tương ứng như hình dưới.

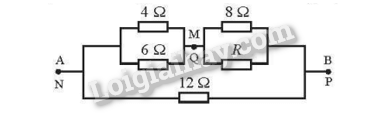
Từ đó tính được R=2Ω

17.9

Đề bài:

Một dây dẫn đồng chất, tiết diện đều có điện trở R₀ được uốn và hàn thành vòng tròn kín với A và B là hai đầu của một đường kính vòng tròn đó.

a) Gọi M và N là hai đầu của một đường kính khác của vòng dây sao cho MN vuông góc với AB. Nối M và N bởi một đoạn dây dẫn có điện trở không đáng kể. Tính điện trở của đoạn mạch AB theo R₀.

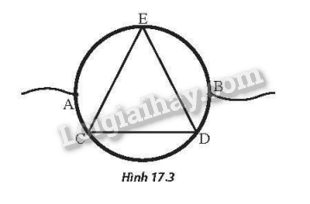
b) Bây giờ không nối tắt giữa M và N như câu a mà người ta dùng một khung dây dẫn kín có dạng một tam giác đều CDE có điện trở không đáng kể mà ba đỉnh luôn tiếp xúc và có thể xoay trượt trên đường tròn (Hình 17.3). Tính điện trở lớn nhất và nhó nhất của đoạn mạch AB theo R₀.

Phương pháp giải

Đọc mạch điện và tính điện trở tương đương

a) Cấu trúc đoạn mạch AB: \(\left( {{R_{{\rm{AM}}}}//{R_{{\rm{AN}}}}} \right){\rm{nt}}\left( {{R_{{\rm{MB}}}}//{{\rm{R}}_{{\rm{NB}}}}} \right)\)

Theo đề, ta có:\({R_{{\rm{AM}}}} = {R_{{\rm{AN}}}} = {R_{{\rm{MB}}}} = {R_{{\rm{NB}}}} = \frac{{{R_0}}}{4}\)

Suy ra, điện trở tương đương của đoạn mạch AB: \({R_{{\rm{AB}}}} = \frac{{{R_0}}}{4}\)

b) Điện trở của các cung tròn CD, DE và EC bằng \(\frac{{{R_0}}}{3}\)

Gọi \({R_{{\rm{AC}}}} = x,{R_{{\rm{DB}}}} = y \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{R_{{\rm{AE}}}} = \frac{{{R_0}}}{3} - x}\\{{R_{{\rm{EB}}}} = \frac{{{R_0}}}{3} - y}\end{array}} \right.\)

Điện trở của đoạn mạch AB: \({R_{{\rm{AB}}}} = \frac{{{R_{{\rm{AE}}}}.{R_{{\rm{AC}}}}}}{{{R_{{\rm{AE}}}} + {R_{{\rm{AC}}}}}} + \frac{{{R_{{\rm{EB}}}}.{R_{{\rm{DB}}}}}}{{{R_{{\rm{EB}}}} + {R_{{\rm{DB}}}}}} = \frac{{x\left( {\frac{{{R_0}}}{3} - x} \right)}}{{\frac{{{R_0}}}{3}}} + \frac{{y\left( {\frac{{{R_0}}}{3} - y} \right)}}{{\frac{{{R_0}}}{3}}}\; = \left( {x + y} \right) - \frac{3}{{{R_0}}}\left( {{{\left( {x + y} \right)}^2} - 2xy} \right)\left( {\rm{*}} \right)\)

Ta có: \(x + y = \frac{{{R_0}}}{2} - \frac{{{R_0}}}{3} = \frac{{{R_0}}}{6}\)

Thay vào phương trình (*), ta được: \({R_{{\rm{AB}}}} = \frac{{{R_0}}}{{12}} + \frac{{6xy}}{{{R_0}}}\)

Vì \(x + y = \frac{{{R_0}}}{6}\) không đổi nên xy lớn nhất khi \(x = y = \frac{{{R_0}}}{{12}} \Rightarrow {R_{{\rm{A}}{{\rm{B}}_{{\rm{max}}}}}} = \frac{{{R_0}}}{8}\)

\({R_{{\rm{A}}{{\rm{B}}_{{\rm{min\;}}}}}} = \frac{{{R_0}}}{{12}}\) khi x hoặc y bằng 0.

17.10

Đề bài:

Mạch điện trở như Hình 17.4 kéo dài đến vô hạn. Biết R₁=4Ω; R₂=3Ω. Tính điện trở tương đương giữa hai đầu A và B.

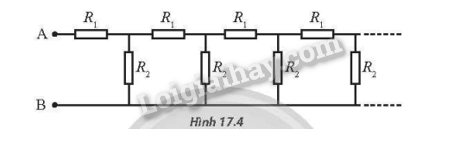
Phương pháp giải

Phân tích mạch điện

Gọi điện trở tương đương giữa hai điểm A và B là R.

Vì mạch kéo dài vô hạn nên điện trở tương đương giữa hai điểm M và N trở đi về phía bên phải (hình bên) (bỏ qua hai điện trở R₁ và R₂ đầu tiên) vẫn bằng R.

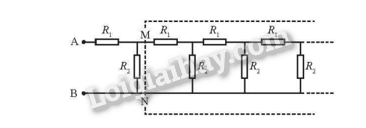
Vì vậy, ta có: \(\frac{{R{R_2}}}{{R + {R_2}}} + {R_1} = R \Rightarrow \frac{{3R}}{{R + 3}} + 4 = R \Rightarrow R = 6{\rm{\Omega }}\)

17.11

Đề bài:

Một chiếc vòng làm bằng một dây dẫn có điện trở R₀=12Ω. Dòng điện đi vào và đi ra khỏi vòng dây tại hai điểm A và B như Hình 17.5. A và B chia vòng dây thành hai phần có chiều dài lần lượt là l₁ và l₂. Tìm tỉ số \(\frac{{{\ell _1}}}{{{\ell _2}}}\) sao cho điện trở của mạch giữa hai điểm A và B là \(R = \frac{8}{3}{\rm{\Omega }}\)

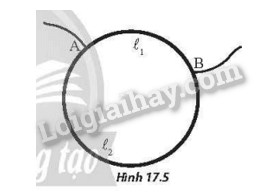
Phương pháp giải

Phân tích mạch điện

Gọi R₁ và R₂ lần lượt là điện trở mỗi phần.

Điện trở tương đương giữa A và B: \(R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{8}{3} \Rightarrow \frac{{{R_1}{R_2}}}{{12}} = \frac{8}{3} \Rightarrow {R_1}{R_2} = 32\)

Vậy, R₁ và R₂ là nghiệm của phương trình: \({x^2} - 12x + 32 = 0\)\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{{\rm{R}}_1} = 8{\rm{\Omega }}}\\{{{\rm{R}}_2} = 4{\rm{\Omega }}}\end{array}} \right.or\left\{ {\begin{array}{*{20}{l}}{{{\rm{R}}_1} = 4{\rm{\Omega }}}\\{{{\rm{R}}_2} = 8{\rm{\Omega }}}\end{array}} \right.\)

Vậy tỉ số \(\frac{{{\ell _1}}}{{{\ell _2}}}\)bằng tỉ số các điện trở tương ứng và bằng 2 hoặc \(\frac{1}{2}\)

17.12

Đề bài:

Một mạch đèn trang trí gồm rất nhiều đèn sợi đốt giống nhau (xem như vô hạn). Các đèn được mắc vào mạch như Hình 17.6. Mỗi đèn coi như một điện trở thuần có giá trị R=2,35Ω. Tìm điện trở tương đương giữa A và B.

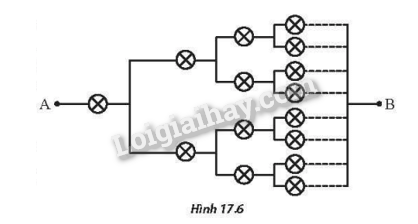
Phương pháp giải

Phân tích mạch điện

Ta có: \(y = \left( {1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \ldots } \right) \Rightarrow y = 1 + \frac{1}{2}\left( {1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \ldots } \right) = 1 + \frac{y}{2} \Rightarrow y = 2\)

Vậy: \({R_{{\rm{AB}}}} = \left( {R + \frac{R}{2} + \frac{R}{4} + \frac{R}{8} + \ldots } \right) = R\left( {1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \ldots } \right) = 2R = 2.2,35 = 4,7{\rm{\Omega }}\)

17.13

Đề bài:

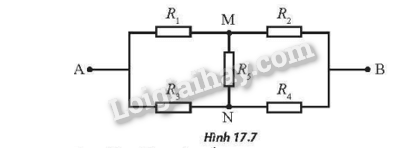
Mạch điện như Hình 17.7 với hai đầu mạch A, B gọi là mạch cầu. Đặt hai đầu A và B vào một hiệu điện thế không đổi U, nếu không có dòng điện chạy qua điện trở R₅ thì khi đó mạch cầu này ở trạng thái được gọi là mạch cầu cân bằng. Chứng minh rằng, điều kiện để mạch cầu cân bằng là: \(\frac{{{R_1}}}{{{R_3}}} = \frac{{{R_2}}}{{{R_4}}}\)

Phương pháp giải

Phân tích mạch điện

Đặt tên các dòng điện như hình bên.

Theo đề: \({I_5} = 0 \Rightarrow {I_1} = {I_2}\) và \({I_3} = {I_4}\left( 1 \right)\)

Ta cũng có: \({U_{{\rm{MN}}}} = 0 \Rightarrow {U_{{\rm{AM}}}} = {U_{{\rm{AN}}}}{\rm{\;;}}{U_{{\rm{MB}}}} = {U_{{\rm{NB}}}}\)

Từ (1), (2) và (3) \( \Rightarrow \frac{{{R_1}}}{{{R_3}}} = \frac{{{R_2}}}{{{R_4}}}\)

17.14

Đề bài:

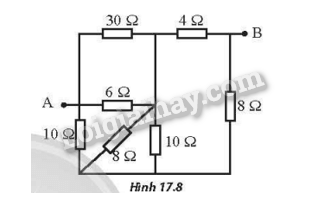
Các điện trở mắc như Hình 17.8. Hãy tính điện trở tương đương giữa hai điểm A và B.

Phương pháp giải

Phân tích mạch điện

Đặt tên các nút như Hình a, sau đó vẽ lại như Hình b.

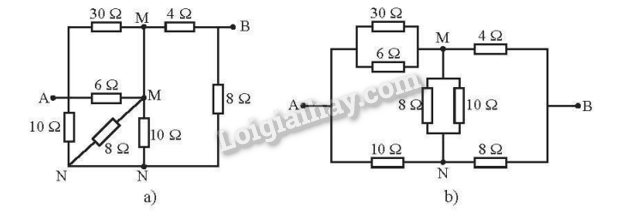
Ta có: \({R_{{\rm{AM}}}} = \frac{{30.6}}{{30 + 6}} = 5{\rm{\Omega }}\)

Vì \(\frac{{{R_{{\rm{AM}}}}}}{{{R_{{\rm{AN}}}}}} = \frac{{{R_{{\rm{MB}}}}}}{{{R_{{\rm{NB}}}}}}\) nên mạch cầu là cân bằng.

Điện trở tương đương của đoạn mạch:

\({R_{{\rm{AB}}}} = \frac{{{R_{{\rm{AM}}}}.{R_{{\rm{AN}}}}}}{{{R_{{\rm{AM}}}} + {R_{{\rm{AN}}}}}} + \frac{{{R_{{\rm{MB}}}}.{R_{{\rm{NB}}}}}}{{{R_{{\rm{MB}}}} + {R_{{\rm{NB}}}}}} = \frac{{5.10}}{{5 + 10}} + \frac{{4.8}}{{4 + 8}} = 6{\rm{\Omega }}\)

17.15

Đề bài:

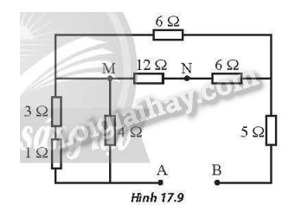
Cho mạch điện như Hình 17.9. Hỏi cần phải đặt vào giữa hai điểm A và B một hiệu điện thế bằng bao nhiêu để hiệu điện thế giữa hai điểm M, N là U_MN=6,0 V

Phương pháp giải

Phân tích mạch điện

Vẽ lại mạch như hình dưới đây.

Ta có: \({R_{{\rm{AM}}}} = \frac{{4.\left( {1 + 3} \right)}}{{4 + 1 + 3}} = 2{\rm{\Omega }};{R_{{\rm{MP}}}} = \frac{{6.\left( {12 + 6} \right)}}{{6 + 12 + 6}} = 4,5{\rm{\Omega }}\)

Theo đề:

\(\begin{array}{l}{U_{{\rm{MN}}}} = 6,0{\rm{\;V}} \Rightarrow {{\rm{I}}_{MN}} = \frac{6}{{12}} = 0,5A\\ \Rightarrow {U_{{\rm{MP}}}} = 0,5.\left( {12 + 6} \right) = 9,0{\rm{\;V}}\\ \Rightarrow {I_{MP}} = \frac{9}{{4,5}} = 2A = {I_{AM}}\\ \Rightarrow {U_{{\rm{AM}}}} = 4{\rm{\;V}};{U_{{\rm{PB}}}} = 10{\rm{\;V}}\end{array}\)

Hiệu điện thế giữa hai điểm A, B: \({U_{{\rm{AB}}}} = {U_{{\rm{AM}}}} + {U_{{\rm{MP}}}} + {U_{{\rm{PB}}}} = 4 + 9 + 10 = 23{\rm{\;V}}\)

17.16

Đề bài:

Các điện trở trong mạch điện ở Hình 17.10 giống nhau và có giá trị R=4Ω. Đặt vào giữa hai đầu A và B một hiệu điện thế U_AB=10 V. Tính cường độ dòng điện trong mạch chính.

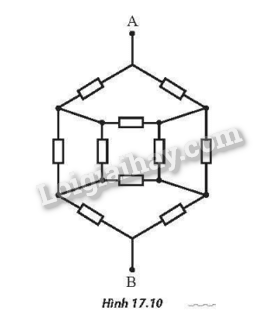
Phương pháp giải

Phân tích mạch điện

Đặt tên các điểm nút như Hình a rồi vẽ lại mạch như Hình b.

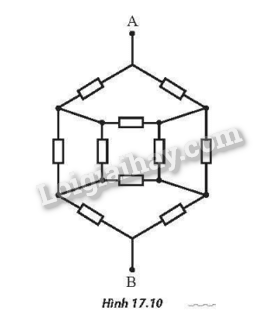
Do tính đối xứng, ta thấy U_ME=U_NF=0 V

Do đó, ta có thể bỏ đi hai điện trở nối vào 2 đầu M, E và N, F.

Điện trở tương đương của đoạn mạch AB: \({R_{{\rm{AB}}}} = \frac{{R.R}}{{R + R}} + \frac{{\frac{{R.R}}{{R + R}}.\frac{{R.R}}{{R + R}}}}{{\frac{{R.R}}{{R + R}} + \frac{{R.R}}{{R + R}}}} + \frac{{R.R}}{{R + R}} = 1,25R = 1,25.4 = 5{\rm{\Omega }}\)

Cường độ dòng điện trong mạch chính:

\(I = \frac{{{U_{{\rm{AB}}}}}}{{{R_{{\rm{AB}}}}}} = \frac{{10}}{5} = 2{\rm{\;A}}\)