
Mẫu số liệu ghi lại cân nặng của 30 học sinh (đơn vị: kilogam):

a) Lập bảng tần số ghép nhóm cho mẫu số liệu trên có tám nhóm ứng với tám nửa khoảng:
[15 ; 20), [20 ; 25), [25 ; 30), [30 ; 35), [35 ; 40), [40 ; 45), [45 ; 50), [50 ; 55)
b) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.
c) Mốt của mẫu số liệu ghép nhóm trên là bao nhiêu?

- Lần lượt đếm số lượng của từng nhóm để lập bảng
- Áp dụng các công thức vừa được học để xác định các đại lượng tiêu biểu

Advertisements (Quảng cáo)
a) Bảng tần số ghép nhóm cho mẫu số liệu trên có tám nhóm ứng với tám nửa khoảng:
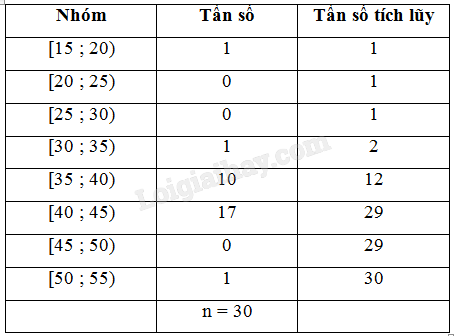
b) Các đại lượng tiêu biểu:
- Trung bình cộng: \(\overline x = \frac{{17,5.1+ 22,5.0 + 27,5.0 + 32,5.1 + 37,5.10 + 42,5.17 + 47,5.0 + 52,5.1}}{{30}} = 40\)
- Trung vị: \({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d = 40 + \left( {\frac{{15 - 12}}{{17}}} \right).5 = 40,88\)
- Tứ phân vị:
+ Tứ phân vị thứ hai \({Q_2} = {M_e} = 40,88\)
+ Tứ phân vị thứ nhất: \({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h = 35 + \left( {\frac{{7,5 - 2}}{{10}}} \right).5 = 37,75\)
+ Tứ phân vị thứ ba: \(Q = t + \left( {\frac{{\frac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right).l = 40 + \left( {\frac{{22,5 - 12}}{{17}}} \right).5 = 43,09\)
c) Mốt của mẫu số liệu:\({M_o} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g = 40 + \left( {\frac{{17 - 10}}{{2.17 - 10 - 0}}} \right).5= 41,46\)
