
Bảng 15 cho ta bảng tần số ghép nhóm số liệu thống kê chiều cao 40 mẫu cây ở một vườn thực vật (đơn vị: centimet).
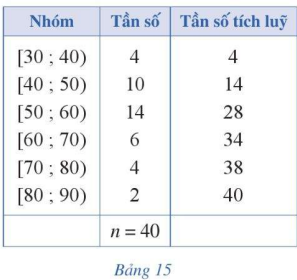
a) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.
b) Mốt của mẫu số liệu ghép nhóm trên là bao nhiêu?

- Áp dụng các công thức vừa được học để xác định các đại lượng tiêu biểu

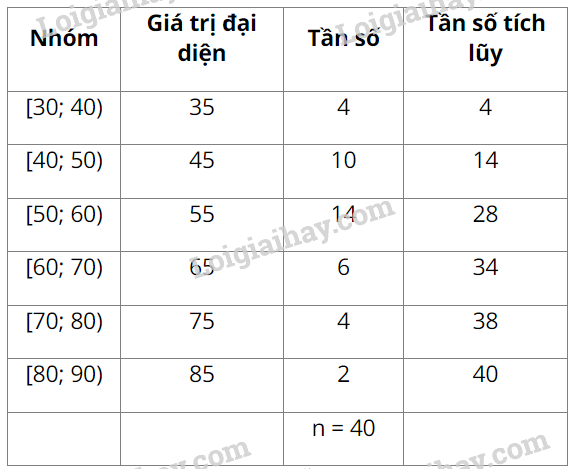
a) Số trung bình cộng của mẫu số liệu ghép nhóm đã cho là:
\(\overline x = \frac{{35.4 + 45.10 + 55.14 + 65.6 + 75.4 + 85.2}}{{40}} = 55,5\)
⦁ Số phần tử của mẫu là n = 40. Ta có: \(\frac{n}{2} = \frac{{40}}{2} = 20\)
Mà \(14 < 20 < 28\) nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 20.
Xét nhóm 3 là nhóm \(\left[ {50;60} \right)\)có \(r = 50,d = 10,{n_3} = 14\) và nhóm 2 là nhóm \(\left[ {40;50} \right)\)có \(c{f_2} = 14\).
Advertisements (Quảng cáo)
Áp dụng công thức, ta có trung vị của mẫu số liệu là:
\({M_e} = 50 + \frac{{20 - 14}}{{14}}.10 \approx 54,29\,(cm)\)
Do đó tứ phân vị thứ hai là \({Q_2} = {M_e} \approx 54,29\,\,(cm)\)
⦁ Ta có: \(\frac{n}{4} = \frac{{40}}{4} = 10\). Mà \(4 < 10 < 14\)nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10.
Xét nhóm 2 là nhóm \(\left[ {40;50} \right)\)có \(s = 40,h = 10,{n_2} = 10\)và nhóm 1 là nhóm \(\left[ {30;40} \right)\)có \(c{f_1} = 4\).
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
\({Q_1} = 40 + \frac{{10 - 4}}{{10}}.10 = 46\,(cm)\)
⦁ Ta có: \(\frac{{3n}}{4} = \frac{{3.40}}{4} = 30\). Mà \(28 < 30 < 34\)nên nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.
Xét nhóm 4 là nhóm \(\left[ {60;70} \right)\)có \(t = 60,l = 10,{n_4} = 6\)và nhóm 3 là nhóm \(\left[ {50;60} \right)\)có \(c{f_3} = 28\).
Áp dụng công thức, ta có tứ phân vị thứ ba là:
\({Q_3} = 60 + \frac{{30 - 28}}{6}.10 \approx 63,33\,(cm)\)
b) Nhóm 3 là nhóm \(\left[ {50;60} \right)\)có tần số lớn nhất với \(u = 50,g = 10,{n_3} = 14\)và nhóm 2 có tần số \({n_2} = 10\), nhóm 4 có tần số \({n_4} = 6\).
Áp dụng công thức, ta có mốt của mẫu số liệu là:
\({M_O} = 50 + \frac{{14 - 10}}{{2.14 - 10 - 6}}.10 \approx 53,33\,(cm)\)
