Hoạt động 4
Xét mẫu số liệu trong Ví dụ 2 được cho dưới dạng bảng tần số ghép nhóm (Bảng 4).
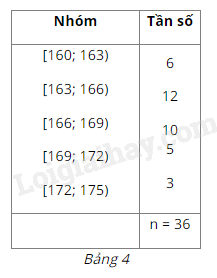
a) Tìm trung điểm \({x_1}\) của nửa khoảng (tính bằng trung bình cộng của hai đầu mút) ứng với nhóm 1. Ta gọi trung điểm \({x_1}\) là giá trị đại diện của nhóm 1.
b) Bằng cách tương tự, hãy tìm giá trị đại diện của bốn nhóm còn lại. Từ đó, hãy hoàn thiện các số liệu trong Bảng 7.
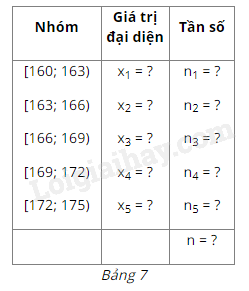
c) Tính giá trị \(\overline x \) cho bởi công thức sau:
\(\overline x = \frac{{{n_1}{x_1} + {n_2}{x_2} + ... + {n_5}{x_5}}}{n}\)

- Tìm trung điểm bằng cách lấy hai đầu mút cộng lại chia 2
- Tìm \(\overline x \) bằng công thức đã cho

a) Trung điểm \(x_1\) (giá trị đại diện) của nửa khoảng ứng với nhóm 1 là:\(x_1 = \frac{160+163}{2} = 161,5 \).b) Giá trị đại diện của nửa khoảng ứng với nhóm 2 là:\(x_2 = \frac{163+166}{2} = 164,5\).Giá trị đại diện của nửa khoảng ứng với nhóm 3 là:\(x_3 = \frac{166+169}{2} = 167,5\).Giá trị đại diện của nửa khoảng ứng với nhóm 4 là:\(x_4 = \frac{169+172}{2} = 170,5\).Giá trị đại diện của nửa khoảng ứng với nhóm 5 là:\(x_5 = \frac{172+175}{2} = 173,5\).Ta hoàn thiện được Bảng 7 như sau: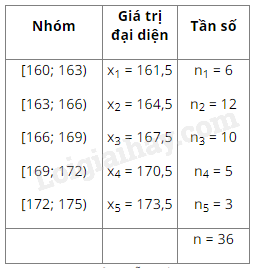
c) Số trung bình cộng của mẫu số liệu đã cho là:
\[\bar{x}=\frac{6\cdot 161,5+12\cdot 164,5+10\cdot 167,5+5\cdot 170,5+3\cdot 173,5}{36}=166,41(6)\]
Advertisements (Quảng cáo)
Luyện tập 4
Xác định số trung bình cộng của mẫu số liệu ghép nhóm trong bài toán ở Luyện tập 2

Dựa vào kiến thức trung vị vừa học để xác định

Trung điểm \({x_1} = 29,5\) là giá trị đại diện của nhóm 1
Trung điểm \({x_2} = 38,5\) là giá trị đại diện của nhóm 2
Trung điểm \({x_3} = 47,5\) là giá trị đại diện của nhóm 3
Trung điểm \({x_4} = 56,5\) là giá trị đại diện của nhóm 4
Trung điểm \({x_5} = 65,5\) là giá trị đại diện của nhóm 5
Trung điểm \({x_6} = 74,5\) là giá trị đại diện của nhóm 6
Trung điểm \({x_7} = 83,5\) là giá trị đại diện của nhóm 7
Trung điểm \({x_8} = 92,5\) là giá trị đại diện của nhóm 8
\({n_1} = 3;{n_2} = 3;{n_3} = 6;{n_4} = 5;{n_5} = 4;{n_6} = 3;{n_7} = 4;{n_8} = 2\)
\( \Rightarrow \overline x = \frac{{29,5.3 + 38,5.3 + 47,5.6 + 56,5.5 + 65,5.4 + 74,5.3 + 83,5.4 + 92,5.2}}{{30}} = 59,2\)
