
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA và SD.
a) Chứng minh rằng (OMN) // (SBC).
b) Gọi P, Q lần lượt là trung điểm của AB, ON. Chứng minh rằng PQ // (SBC).

a) Nếu mặt phẳng (P) chứa 2 đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q).
b) Nếu (P) và (Q) song song với nhau thì mọi đường thẳng trong (P) song song với (Q) và ngược lại.

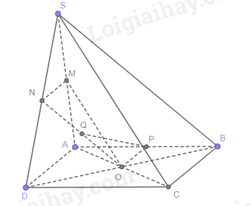
a) O là tâm hình bình hành ABCD. Suy ra O là trung điểm của AC và BD
Xét tam giác SAD có M, N lần lượt là trung điểm của SA, SD nên MN // AD
Advertisements (Quảng cáo)
Mà AD // BC (Do ABCD là hình bình hành) nên MN // BC
Suy ra MN // (SBC) (1)
Xét tam giác SAC có M, O lần lượt là trung điểm của SA, AC nên MO // SC
Suy ra MO // (SBC) (2)
Từ (1) và (2) suy ra (MNO) // (SBC)
b) Xét tam giác ABC có O, P lần lượt là trung điểm của AC, AB nên OP // BC
Suy ra OP // (SBC) (3)
Xét tam giác SBD có O, N lần lượt là trung điểm của BD, SD nên ON // SB
Suy ra ON // (SBC) hay OQ // (SBC) (4)
Từ (3) và (4) suy ra (OPQ) // (SBC)
Nên PQ // (SBC).
