
Trong mặt phẳng (P), cho hình bình hành ABCD. Lấy S nằm ngoài mặt phẳng (P). Lấy M, N lần lượt là các điểm nằm trên các cạnh SA, SC.
a) Chứng minh rằng đường thẳng MN nằm trong mặt phẳng (SAC).
b) Giả sử MN và AC cắt nhau tại I, chứng minh I là điểm chung của hai mặt phẳng (BMN) và (ABC), từ đó suy ra giao tuyển của hai mặt phẳng (BMN) và (ABC).

a) Đường thẳng có 2 điểm phân biệt nằm trong mặt phẳng thì đường thẳng đó cũng thuộc vào mặt phẳng.
b) Nếu 2 điểm A, B cùng thuộc 2 mặt phẳng phân biệt (P) và (Q) thì AB là giao tuyến của (P) và (Q).

Advertisements (Quảng cáo)
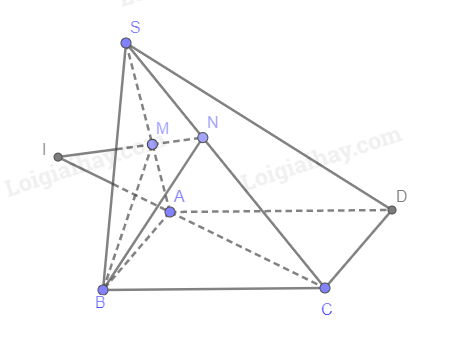
a)
\(\left\{ \begin{array}{l}M \in SA\\N \in SC\end{array} \right. \Rightarrow MN \subset \left( {SAC} \right)\)
b)
\(\begin{array}{l}I = MN \cap AC\\\left\{ \begin{array}{l}MN \subset \left( {BMN} \right)\\AC \subset \left( {ABC} \right)\end{array} \right.\end{array}\)
Nên I là điểm chung của (BMN) và (ABC)
\( \Rightarrow BI = \left( {BMN} \right) \cap \left( {ABC} \right)\).
