
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N, P lần lượt là các điểm nằm trên AA’, AB, DC sao cho \(\frac{{AM}}{{AA’}} = \frac{{AN}}{{AB}} = \frac{{DP}}{{DC}} = \frac{1}{3}\).
a) Chứng minh mặt phẳng (MNP) song song với (A’BC).
b) Gọi Q là giao điểm của AC’ với (MNP). Xét vị trí tương đối của MQ và A’C.

a) (P) chứa 2 đường thẳng cắt nhau lần lượt song song với (Q) thì (P) // (Q).
b) Tìm giao điểm của đường thẳng a và mặt phẳng (P):
+ Bước 1: Chọn 1 mặt phẳng (Q) chứa a. Tìm giao tuyến d của (P) và (Q)
+ Bước 2: Tìm giao điểm I của a và d. I chính là giao điểm của a và (P).

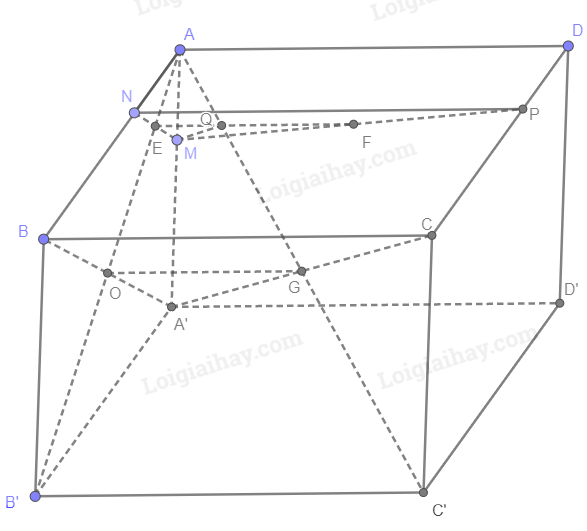
a) Xét tam giác ABA’ có \(\frac{{AM}}{{AA’}} = \frac{{AN}}{{AB}} = \frac{1}{3}\) nên MN // A’B. Suy ra MN // (A’BC) (1)
Xét hình bình hành ABCD có \(\frac{{AN}}{{AB}} = \frac{{DP}}{{DC}} = \frac{1}{3}\) nên NP // BC. Suy ra NP // (A’BC) (2)
Advertisements (Quảng cáo)
Từ (1), (2) suy ra (MNP) // (A’BC)
b) Trong (ABB’A’), gọi E là giao điểm của AB’ và MN
Suy ra E là điểm chung của (AB’C’) và (MNP). Mà NP // B’C’ (cùng // BC)
Qua E kẻ đường thẳng d song song với NP và B’C’, cắt EP tại F. Suy ra EF là giao tuyến của (MNP) và (AB’C’)
Trong (AB’C’), gọi Q là giao điểm của EF và AC’
Vậy Q là giao điểm của AC’ và (MNP)
Trong (ABB’A’), gọi O là giao điểm của A’B và AB’
Xét tam giác ABO có NE // BO nên \(\frac{{AN}}{{AB}} = \frac{{AE}}{{AO}} = \frac{1}{3}\)
Ta có: AA’ // CC’ (cùng // BB’) và AA’ = CC’ (cùng bằng BB’) nên ACC’A’ là hình bình hành
Trong (AA’C’C), gọi G là giao điểm của AC’ và A’C. Suy ra G là trung điểm của AC’ và A’C
Xét tam giác AB’C’ có O, G là trung điểm của AB’, AC’ nên OG // B’C’. Suy ra OG // NQ \( \Rightarrow \frac{{AE}}{{AO}} = \frac{{AQ}}{{AG}} = \frac{1}{3}\)
Xét tam giác AA’G có: \(\frac{{AM}}{{AA’}} = \frac{{AQ}}{{AG}} = \frac{1}{3} \Rightarrow MQ\,{\rm{// }}A’G\) hay MQ // A’C.
