
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SCD.
a) Tim giao tuyến của hai mặt phẳng (SBG) và (SAC).
b) Tìm giao điểm của đường thằng BG và mặt phẳng (SAC).

a) Tìm giao tuyến của hai mặt phẳng (P) và (Q)
Tìm 2 điểm chung A, B của 2 mặt phẳng đó. AB chính là giao tuyến của (P) và (Q).
b) Tìm giao điểm của đường thẳng d và mặt phẳng (P)
Cách 1: Nếu (P) có chứa đường thẳng cắt d
Cách 2: Nếu (P) không chứa đường thẳng cắt d
+ Bước 1: Tìm \(\left( Q \right) \supset d\) và \(\left( P \right) \cap \left( Q \right) = a\)
Advertisements (Quảng cáo)
+ Bước 2: Tìm \(I = a \cap d \Rightarrow I = d \cap \left( P \right)\)

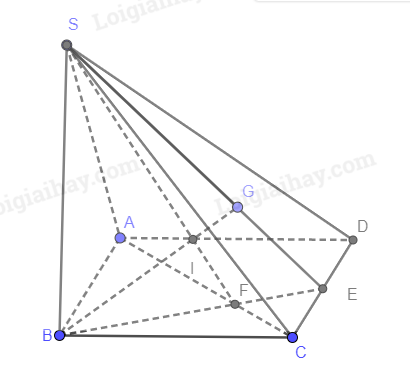
a) Gọi E là trung điểm của CD
Mà G là trọng tâm tam giác SCD nên G nằm trên SE.
Mở rộng (SBG) thành (SBE)
Trong (ABCD), gọi \(AC \cap BE = F\)
\(\begin{array}{l}\left\{ \begin{array}{l}AC \subset \left( {SAC} \right)\\BE \subset \left( {SBE} \right)\end{array} \right.\\ \Rightarrow F \in \left( {SAC} \right) \cap \left( {SBE} \right)\end{array}\)
\(\begin{array}{l} \Rightarrow SF = \left( {SAC} \right) \cap \left( {SBE} \right)\\ \Rightarrow SF = \left( {SAC} \right) \cap \left( {SBG} \right)\end{array}\)
b) Trong (SBE), gọi \(SF \cap AC = I\)
Mà: \(\left\{ \begin{array}{l}\left( {SAC} \right) \cap \left( {SBG} \right) = SF\\AC \subset \left( {SAC} \right)\end{array} \right. \Rightarrow I = BG \cap \left( {SAC} \right)\)
