Hoạt động 2
Cho đường thẳng d và điểm M không thuộc d. Vẽ đường thẳng d’ qua M và song song với d.
a) Đường thẳng d’ có nằm trong mặt phẳng (M, d) không?
b) Có thể vẽ được bao nhiêu đường thẳng d’ như vậy? Vì sao?

a) Hai đường thẳng song song là hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung.
b) Sử dụng tiên đề Euclid: “Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.”

a) Đường thẳng d’ nằm trong mặt phẳng (M, d) vì hai đường thẳng song song phải đồng phẳng.
b) Chỉ vẽ được duy nhất một đường thẳng d’ vì theo tiên đề Euclid: “Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.”
Hoạt động 3
Cho hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) cắt nhau theo giao tuyến c. Một mặt phẳng \(\left( \gamma \right)\) cắt \(\left( \alpha \right)\) và \(\left( \beta \right)\) lần lượt theo các giao tuyến a và b.
a) Khi a và b cắt nhau tại I thì I có thuộc c không?
b) Khi a và b song song với nhau thì a có thể cắt đường thẳng c không?

Điểm chung của 2 mặt phẳng thì phải nằm trên giao tuyến của chúng.

a)
\(\left\{ \begin{array}{l}a \subset \left( \alpha \right)\\b \subset \left( \beta \right)\\a \cap b = I\end{array} \right.\)
Nên I là điểm chung của \(\left( \alpha \right)\) và \(\left( \beta \right)\).
Mà c là giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\).
Vậy I phải thuộc c.
b) Giả sử a và c cắt nhau tại điểm O. Ta có:
\(\left\{ \begin{array}{l}a \cap c = O\\a \subset \left( \gamma \right)\\c \subset \left( \beta \right)\end{array} \right.\)
\( \Rightarrow \)O là điểm chung của \(\left( \gamma \right)\) và \(\left( \beta \right)\). Mà b là giao tuyến của \(\left( \gamma \right)\) và \(\left( \beta \right)\).
\( \Rightarrow \)\(O \in b\)
Mặt khác: \(O \in a\)
\( \Rightarrow \)a và b có điểm chung là O (Mâu thuẫn với a song song với b)
Vậy a không thể cắt c.
Luyện tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M là một điểm thuộc đoạn SA (M khác S và A). Xác định giao tuyến của các mặt phẳng (SAB) và (MCD).

Hai mặt phẳng (P) và (Q) có điểm chung là A và lần lượt chứa 2 đường thẳng song song là a và b thì giao tuyến của chúng sẽ là đường thẳng đi qua A và song song với a, b.

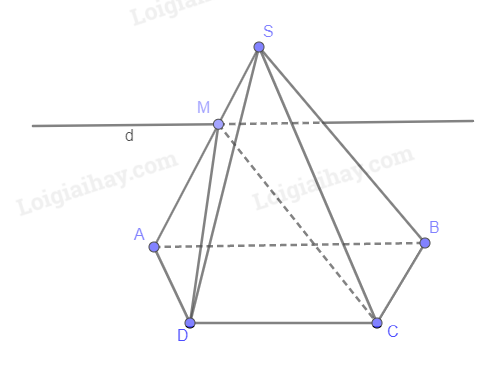
(SAB) và (MCD) có điểm chung là M và lần lượt chứa hai đường thẳng song song là AB và CD nên giao tuyến của chúng là đường thẳng d đi qua M và song song với AB, CD.
Luyện tập 3
Cho hình chóp S.ABC. Gọi I và J lần lượt là trung điểm của AB và AC. (P) là mặt phẳng chứa IJ và cắt SB, SC lần lượt tại K, L. Chứng minh rằng IJLK là hình thang. Nếu K là trung điểm SB thì tứ giác IJLK là hình gì?

Áp dụng hệ quả định lý về giao tuyến của 3 mặt phẳng:
\(\left\{ \begin{array}{l}a \subset \left( P \right)\\b \subset \left( Q \right)\\a//b\\\left( P \right) \cap \left( Q \right) = c\end{array} \right. \Rightarrow a//b//c\)
Nhắc lại kiến thức cũ:
Advertisements (Quảng cáo)
- Hình thang là tứ giác có 2 cạnh đối song song với nhau. Hình thang có 2 cạnh đáy bằng nhau là hình bình hành.
- Đường trung bình của tam giác là đoạn thẳng nối trung điểm 2 cạnh của tam giác. Đường trung bình song song với cạnh thứ ba và bằng nửa cạnh ấy.

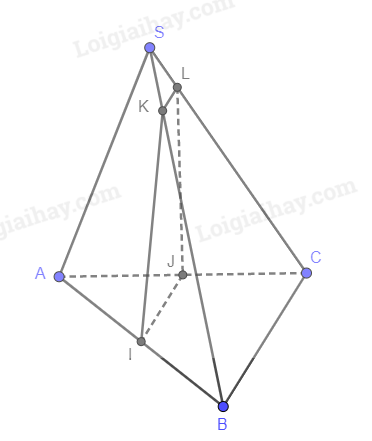
Ta có: IJ song song với BC vì cùng thuộc (ABC) và không có điểm chung (Đường trung bình trong tam giác)
Theo đề bài: \(\left( P \right) \cap \left( {SBC} \right) = KL\)
Mà (P) và (SBC) lần lượt có IJ và BC song song với nhau nên KL cũng song song với IJ, BC.
Vậy IJLK là hình thang.
Nếu K là trung điểm của SB thì KL song song với BC và bằng \(\frac{1}{2}\)BC
Mặt khác: IJ cũng bằng \(\frac{1}{2}\)BC (Đường trung bình trong tam giác)
Nên KL = IJ
Hình thang IJLK có KL = IJ là hình bình hành.
Hoạt động 4
Quan sát hình một cánh cửa. Khung cửa là một hình chữ nhật và \({d_1},{d_2}\) là hai đường thẳng chứa hai cạnh hình chữ nhật, mép cửa là hình ảnh đường thẳng \(\Delta \) (Hình 4.48). Khi cánh cửa xoay, hãy nhận xét về vị trí tương đối giữa \(\Delta \)với \({d_1}\)?
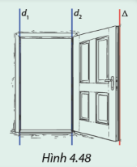

Quan sát hình vẽ.

Khi cánh cửa xoay thì \(\Delta \)và \({d_1}\) song song với nhau hoặc trùng nhau.
Luyện tập 4
Cho hình chóp S.ABCD có đáy là tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AB, AD, SD, SB. Chứng minh rằng MNPQ là hình bình hành.

- Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
- Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành.
- Đường trung bình là đoạn thẳng nối trung điểm của 2 cạnh tam giác. Đường trung bình song song và bằng một nửa cạnh thứ ba.

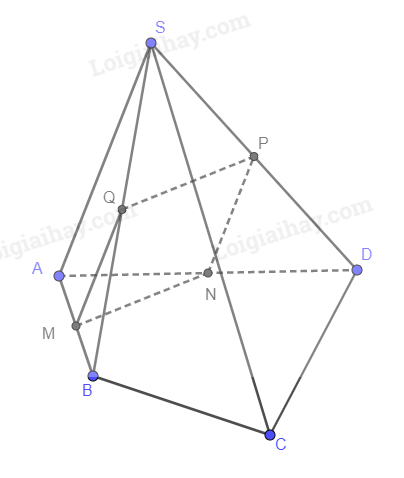
Xét (SAB) có M, Q lần lượt là trung điểm của AB, SB nên MQ song song và bằng một nửa SA.
Xét (SAD) có P, N lần lượt là trung điểm của SD, AD nên PN song song và bằng một nửa SA.
Suy ra MQ và PN song song và bằng nhau.
Vậy MNPQ là hình bình hành.
Vận dụng
a) Hình 4.51 là một loại thang nhôm chữ A được kết hợp từ hai nhánh là hai thang đơn. Hãy chỉ ra hình ảnh một số cặp đường thẳng song song ở mỗi nhánh của thang. Các bậc thang ở hai nhánh khác nhau có song song với nhau không? Vì sao?
b) Hãy nêu thêm một số đồ vật xung quanh có hình ảnh là các đường thẳng song song.


Hai đường thẳng song song là hai đường thẳng đồng phẳng và không có điểm chung.

a) Các bậc thang ở một nhánh đều song song với nhau.
Vì các bậc thang ở mỗi nhánh đều song song với bậc thang trên cùng của nhánh đó. Mà 2 bậc thang trên cùng song song với nhau nên các bậc thang ở hai nhánh khác nhau cũng song song với nhau.
b) Các hình ảnh có các đường thẳng song song là sàn nhà có lát gạch, bảng, bàn, ghế,…
