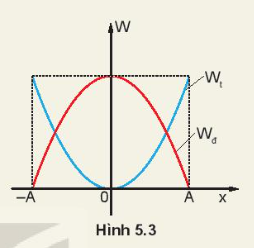
1. Hình 5.3 là đồ thị động năng và thế năng của một vật dao động điều hòa li độ. Hãy phân tích sự chuyển hóa giữa động năng và thế năng bằng đồ thị
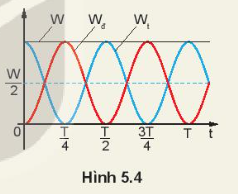
2. Hình 5.4 là đồ thị động năng và thế năng của một vật dao động điều hòa theo thời gian.
a) Động năng và thế năng của vật thay đổi như thế nào trong các khoảng thời gian: từ 0 đến \(\frac{T}{4}\), từ \(\frac{T}{4}\)đến \(\frac{T}{2}\), từ \(\frac{T}{2}\)đến \(\frac{{3T}}{4}\), từ \(\frac{{3T}}{4}\)đến T.
b) Tại các thời điểm: t = 0; t = \(\frac{T}{8}\); t =\(\frac{T}{4}\); t = \(\frac{{3T}}{8}\), động năng và thế năng của vật có giá trị như thế nào (tính theo W). Nghiệm lại để thấy ở mỗi thời điểm đó Wđ + Wt = W.

Dựa vào nội dung kiến thức đã học về động năng và thế năng để trả lời

1.
Khi vật di chuyển từ biên âm đến vị trí cân bằng thì thế năng giảm động năng tăng và ngược lại.
Khi vật đi chuyển từ vị trí cân bằng đến biên dương thì thế năng tăng động năng giảm và ngược lại.
Advertisements (Quảng cáo)
Vật đạt động năng cực đại khi ở vị trí cân bằng và cực tiểu khi ở vị trí biên còn thế năng thì ngược lại.
2.
a) Từ 0 đến \(\frac{T}{4}\): Wđ tăng từ 0 đến giá trị lớn nhất tại \(\frac{T}{4}\), Wt giảm từ giá trị lớn nhất về 0 tại \(\frac{T}{4}\).
Từ \(\frac{T}{4}\)đến \(\frac{T}{2}\): Wđ giảm từ giá trị lớn nhất về 0 tại \(\frac{T}{2}\), Wt tăng từ 0 đến giá trị lớn nhất tại \(\frac{T}{2}\).
Từ \(\frac{T}{2}\)đến \(\frac{{3T}}{4}\): Wđ tăng từ 0 đạt giá trị lớn nhất tại \(\frac{{3T}}{4}\),Wt giảm từ giá trị lớn nhất về 0 tại \(\frac{{3T}}{4}\).
Từ \(\frac{{3T}}{4}\)đến T: Wđ giảm từ giá trị lớn nhất về 0 tại T, Wt tăng từ 0 đến giá trị lớn nhất tại T.
b) Tại thời điểm t = 0: Wđ = 0, Wt = W.
Tại thời điểm t = \(\frac{T}{8}\): Wđ = Wt = \(\frac{{\rm{W}}}{2}\).
Tại thời điểm t = \(\frac{T}{4}\): Wđ = W, Wt = 0.
Tại thời điểm t = \(\frac{{3T}}{8}\): Wđ = Wt = \(\frac{{\rm{W}}}{2}\).
→ ở mỗi thời điểm trên ta đều có: Wđ + Wt = W.
