Một con lắc lò xo có vật nặng khối lượng 0, 4 kg, dao động điều hòa. Đồ thị vận tốc v theo thời gian t như hình 5. 7...

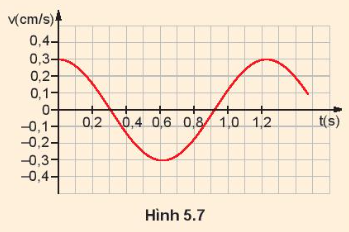
1. Một con lắc lò xo có vật nặng khối lượng 0,4 kg, dao động điều hòa. Đồ thị vận tốc v theo thời gian t như hình 5.7. Tính:

a) Vận tốc cực đại của vật.

b) Động năng cực đại của vật.

c) Thế năng cực đại của con lắc.

d) Độ cứng k của lò xo.

2. Một con lắc lò xo có độ cứng k = 100 N/m, vật nặng có khối lượng m = 200 g, dao động điều hòa với biên độ A = 5 cm.

a) Xác định li độ của vật tại thời điểm động năng của vật bằng 3 lần thế năng của con lắc.

b) Xác định tốc độ của vật khi qua vị trí cân bằng.

c) Xác định thế năng của con lắc khi vật có li độ x = -2,5 cm

1. Dựa vào các công thức tính chu kỳ, vận tốc, động năng và thế năng để trả lời

2. Dựa vào các công thức của con lắc lò xo để trả lời

1.

Từ đồ thị ta có T = 1,2s → \(\omega = \frac{{2\pi }}{T} = \frac{5}{3}\pi \) (rad/s)

a) Vận tốc cực đại của vật v_max = 0,3 cm/s= 0,003 m/s = ωA → A = 0.0006 (m)

b) Động năng cực đại của vật là W_đmax = = 2.10⁻⁶ (J)

c) Theo định luật bảo toàn cơ năng ta có W_tmax = W_đmax = 2.10⁻⁶ (J)

d) Độ cứng k của lò xo tính theo công thức: T = \(2\pi \sqrt {\frac{m}{k}} \) → k≈11N/m

2.

Ta có:

Độ cứng k = 100 N/m

Khối lượng m = 200 g = 0,2 kg

Biên độ A = 5 cm = 0,05 m

a) W_đ = 3 W_t

Theo định luật bảo toàn cơ năng W = W_đ + W_t = 4W_t

\( \to \frac{1}{2}m{\omega ^2}{A^2} = 4\frac{1}{2}m{\omega ^2}{x^2} \to x = \pm 2,5(cm)\)

b) Tần số góc ω = \(\sqrt {\frac{k}{m}} = 10\sqrt 5 \) (rad/s)

Khi vật đi qua vị trí cân bằng vật có tốc độ lớn nhất

V = ωA = 0,05. \(10\sqrt 5 \) = \(\frac{{\sqrt 5 }}{2}\) (m/s)

c) W_t1 = \(\frac{1}{2}m{\omega ^2}{x^2}\) = 1562,5 (s).