Một lăng kính thuỷ tinh có chiết suất n = 1,5; tiết diện chính là một tam giác đều, được đặt trong không khí.
a) Tính góc lệch của tia sáng qua lăng kính khi góc tới là 30°.
b) Vẽ đường đi tia sáng và tính góc mà tia ló hợp với tia tới trong trường hợp tia tới vuông góc với mặt bên của lăng kính.

a) Ta có A = 60°, n = 1,5; lăng kính đặt trong không khí.
Theo giả thiết i = 30° \(\Rightarrow {\mathop{\rm s}\nolimits} {\rm{inr}} = {{{\mathop{\rm s}\nolimits} {\rm{ini}}} \over n} = {{\sin {{30}^0}} \over {1,5}} = 0,333 \Rightarrow r = {19^0}28’\)
Ta có: r’ = A - r = 60 - 19°28′ = 40°32′
\(\Rightarrow\) \(\sin i’ = n\sin r’ \)= 1,5sin40°32′ = 0,975 \(\Rightarrow\) i’ = 77°
Vậy góc lệch D = i + i’ - A = 30° + 77° - 60° = 47°
b)
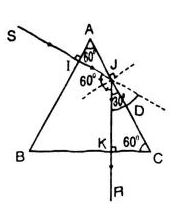
Trường hợp cho tia tới SI vuông góc với mặt bên lăng kính
Tia sáng đi từ không khí vào lăng kính:
Advertisements (Quảng cáo)
n1= 1, n2 = 1,5
\(SI \bot AB\) \(\Rightarrow\) i = 0°
\( \Rightarrow {\mathop{\rm s}\nolimits} {\rm{inr}} = {{\sin i} \over n_2} = {0 \over {1,5}} = 0 \Rightarrow r = 0\)
Tia IJ truyền thẳng đến mặt AC.
Tia sáng đi từ lăng kính ra không khí:
n1 = 1,5, n2 = 1
Ta có: \(\sin {i_{gh}} = {{{n_2}} \over {{n_1}}} = {1 \over {1,5}} \Rightarrow {i_{gh}} = {42^{0.}}\)
Góc tới i = 60° >igh nên có sự phản xạ toàn phần, tia JK là tia phản xạ.
Tia sáng đi từ lăng kính ra không khí: n1 = 1,5, n2 = 1
Ta có tia tới \(JK \bot BC\) nên i = 0 \(\Rightarrow\) r = 0
Tia ló KR truyền thẳng ra ngoài không khí
Dựa vào hinh vẽ ta tính được góc lệch D = 60°.
