II.17. Ở mặt thoáng của một chất lỏng có hai nguồn sóng kết hợp A và B cách nhau 20 cm, dao động theo phương thẳng đứng với phương trình uA = 2cos40\(\pi\)t và uB = 2cos(40\(\pi\)t + \(\pi\)) (uA và uB tính bằng mm, t tính bằng s). Biết tốc độ truyền sóng trên mặt chất lỏng là 30 cm/s. Xét hình vuông AMNB thuộc mặt thoáng của chất lỏng. Hỏi số điểm dao động với biên độ cực đại trên đường chéo BM của hình vuông là bao nhiêu ?
Hướng dẫn giải chi tiết
Xem Hình II.5G.
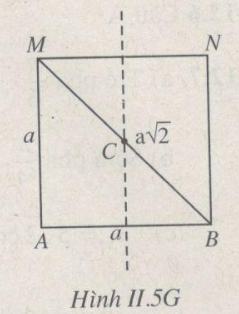
Trước hết ta tìm số vân cực đại trên toàn mặt thoáng. Đó cũng là số vân cực đại trên đoạn AB. Vì hai nguồn kết hợp dao động ngược pha nên ta có :
\(\eqalign{
& {d_2} - {d_1} = \left( {k + {1 \over 2}} \right)\lambda \cr
& = \left( {k + {1 \over 2}} \right){v \over f} = \left( {k + {1 \over 2}} \right){3 \over 2}\left( {cm} \right) \cr
& {d_2} + {d_1} = 20\left( {cm} \right) \Rightarrow {d_2} = 10 + \left( {k + {1 \over 2}} \right){3 \over 4}\left( {cm} \right) \cr} \)
Advertisements (Quảng cáo)
Vì 0 < d2 < 20 (cm) ⇒ k = -13.. -12, -1,0, 1. 12
Bây giờ ta xét số vân cực đại trên đoạn BM.
-20 < d2 - d1 < 20(\(\sqrt2\) - 1) (cm)
\( - 20 < \left( {k + {1 \over 2}} \right){3 \over 2} \le 2 - \left( {\sqrt 2 - 1} \right)\)
⇒ k = -13, -12 ...-1.0, 1.. 5 ⇒ 19 điểm.
