Hoạt động (HĐ) 2
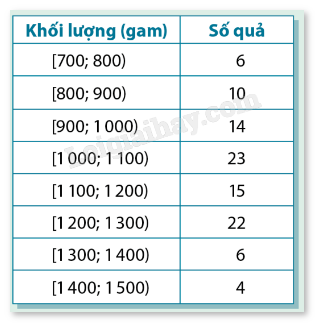
Trở lại với bảng 3.1 về khối lượng của 100 quả dứa giống E. Để tiện tính toán, ta biểu diễn dữ liệu bằng một bảng hai cột như bảng trên.
a) Hãy tính các tứ phân vị của mẫu số liệu cho trong bảng.
b) Đề xuất một cách ước tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho.

a) Sử dụng công thức tính tứ phân vị:
\({Q_x} = L + \left( {\frac{{{n_x} - F}}{f}} \right) \times h\)
Trong đó:
- \({Q_x}\) là giá trị tứ phân vị cần tìm \(\left( {{Q_1},{Q_2}} \right.\), hoặc \(\left. {{Q_3}} \right)\).
- \(L\) là cận dưới của khoảng chứa tứ phân vị.
- \({n_x}\) là vị trí của tứ phân vị trong tổng số mẫu (ví dụ, \({n_{{Q_1}}} = \frac{N}{4}\) cho \({\rm{Q}}1,{n_{{Q_2}}} = \frac{N}{2}\) cho Q2).
- \(F\) là tần suất tích lũy của khoảng liền trước khoảng chứa tứ phân vị.
- \(f\) là tần suất của khoảng chứa tứ phân vị.
- \(h\) là độ dài của khoảng giá trị (ví dụ: từ 900 đến 1000 thì \(h = 100\)).
b) Khoảng tứ phân vị là khoảng giữa \({Q_3}\) và \({Q_1}\), ký hiệu là: \({\Delta _Q} = {Q_3} - {Q_1}\).

a) Tính tần số tích luỹ
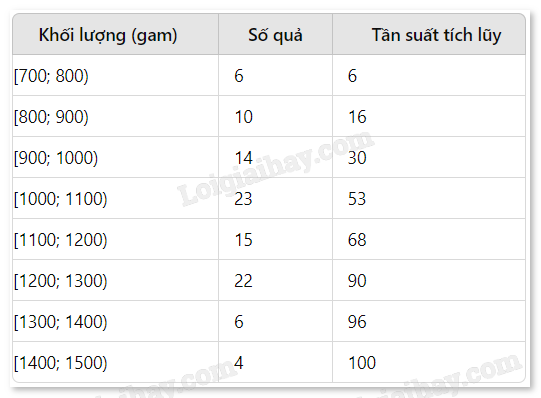
Kích thước của mẫu số liệu là \(N = 100\). Ta có \(\frac{N}{4} = 25;\frac{{2N}}{4} = 50;\frac{{3N}}{4} = 75\)
Nhóm chứa \({Q_1}\) là [900; 1000)
\({Q_1} = 900 + \frac{{25 - 16}}{{14}} \times 100 \approx 964,29{\rm{ gam}}\)
Nhóm chứa \({Q_2}\) là [1000; 1100)
\({Q_2} = 1000 + \frac{{50 - 30}}{{23}} \times 100 \approx 1086,96{\rm{ gam}}\)
Nhóm chứa \({Q_3}\) là [1200; 1300)
\({Q_3} = 1200 + \frac{{75 - 68}}{{22}} \times 100 \approx 1231,82{\rm{ gam}}\)
b) Khoảng tứ phân vị là: \({\Delta _Q} = {Q_3} - {Q_1} = 1231,82 - 964,29 = 267,53\)
Luyện tập (LT) 3
Ở một phòng điều trị nội trú của bệnh viện, dữ liệu thống kê thời gian ngủ hằng đêm của hai bệnh nhân trong suốt một tháng được tổng hợp bởi hai bảng dưới đây:
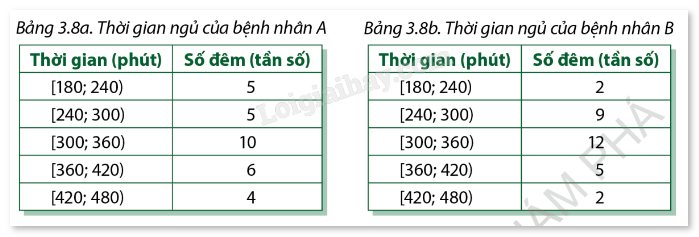
Bệnh nhân nào có thời gian ngủ ổn định hơn?

Tính tần suất tích lũy cho cả hai bệnh nhân.
Xác định \({Q_1}\), \({Q_2}\), và \({Q_3}\) cho mỗi bệnh nhân.
Tính khoảng tứ phân vị \({\Delta _Q}\) cho mỗi bệnh nhân.
So sánh khoảng tứ phân vị \({\Delta _Q}\) của hai bệnh nhân. Bệnh nhân có \({\Delta _Q}\) nhỏ hơn sẽ có thời gian ngủ ổn định hơn.

- Bệnh nhân A:
Tính tần suất tích luỹ:
Advertisements (Quảng cáo)
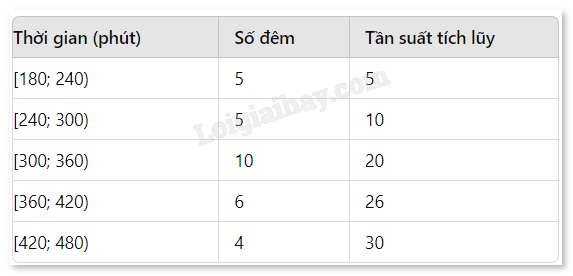
Tính tứ phân vị:
\({Q_1} = 240 + \frac{{7.5 - 5}}{5} \times 60 = 240 + 30 = 270\) phút
\({Q_2} = 300 + \frac{{15 - 10}}{{10}} \times 60 = 300 + 30 = 330\) phút
\({Q_3} = 360 + \frac{{22.5 - 20}}{6} \times 60 = 360 + 25 = 385\) phút
Khoảng tứ phân vị là:
\(\Delta _Q^A = {Q_3} - {Q_1} = 385 - 270 = 115\) phút
- Bệnh nhân B:
Tính tần suất tích luỹ:
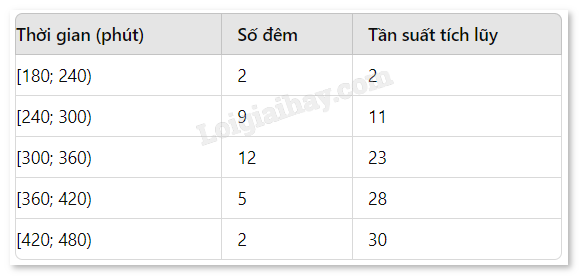
Tính tứ phân vị:
\({Q_1} = 240 + \frac{{7.5 - 2}}{9} \times 60 = 240 + 36,67 = 276,67\) phút
\({Q_2} = 300 + \frac{{15 - 11}}{{12}}.60 = 320\) phút
\({Q_3} = 300 + \frac{{22.5 - 11}}{{12}} \times 60 = 300 + 57,5 = 357,5\) phút
Khoảng tứ phân vị là:
\(\Delta _Q^B = {Q_3} - {Q_1} = 357.5 - 276.67 = 80.83\) phút
Vì \(\Delta _Q^B
Luyện tập (LT) 4
Hình 3.3 là biểu đồ biểu diễn nhiệt độ trung bình hằng tháng của hai địa phương Y, Z.
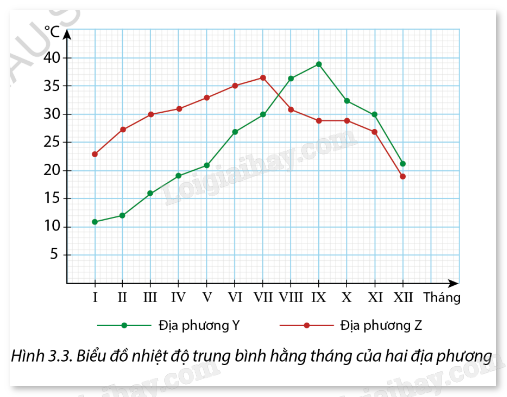
a) Lập bảng số liệu ghép nhóm về nhiệm độ của hai địa phương Y, Z, với độ dài các nhóm là 5 và đầu mút phải của nhóm cuối cùng là 40.
b) Tìm khoảng tứ phân vị của nhiệt độ mỗi địa phương và cho biết nhiệt độ của địa phương nào ít biến động hơn.

a)
- Tạo bảng với các hàng tương ứng với các khoảng nhiệt độ (5-10, 10-15, ..., 35-40) và hai cột tương ứng với địa phương Y và Z.
- Đếm số lượng tháng mà nhiệt độ trung bình rơi vào mỗi khoảng nhiệt độ cho từng địa phương.
b)
- Xác định khoảng tứ phân vị.
- Địa phương nào có khoảng tứ phân vị nhỏ hơn thì nhiệt độ của địa phương đó biến động ít hơn.

Đọc số liệu từ biểu đồ:
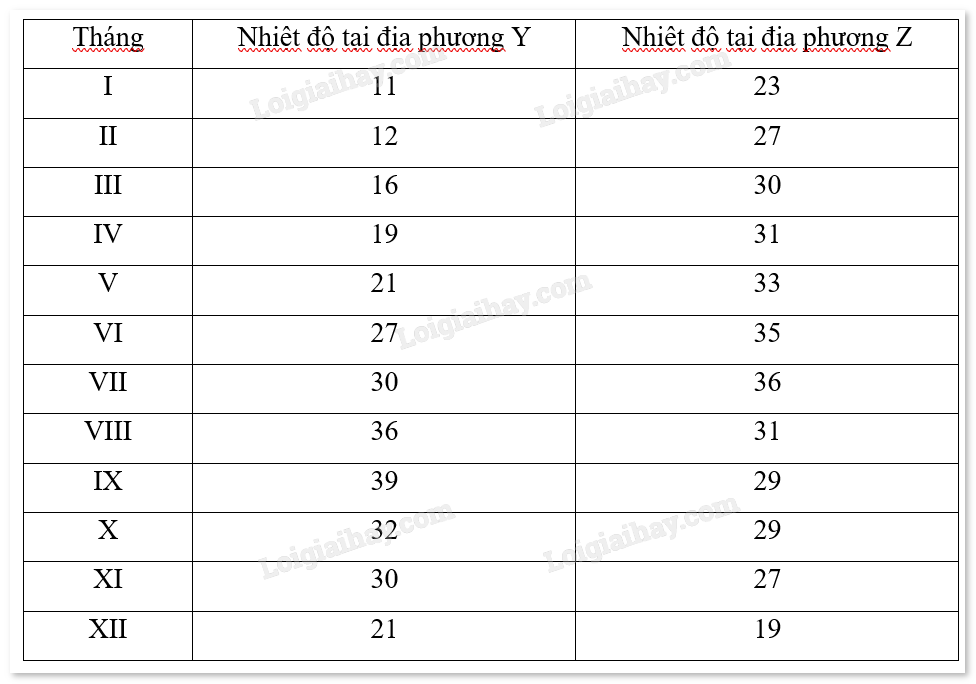
Lập bảng số liệu ghép nhóm:
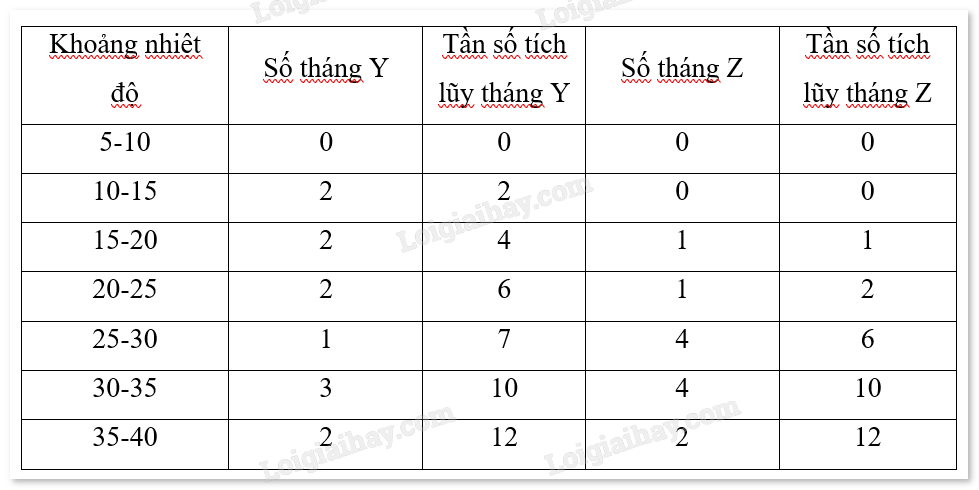
b) Tính khoảng tứ phân vị và so sánh
\(Q_1^Y = 15 + \frac{{3 - 2}}{2}.5 = 17,5;Q_3^Y = 30 + \frac{{9 - 7}}{3}.5 = 33,3\)
\(Q_1^Z = 25 + \frac{{3 - 2}}{4}.5 = 26,25;Q_3^Z = 30 + \frac{{9 - 6}}{4}.5 = 33,75\)
\(\begin{array}{l}\Delta _Q^Y = Q_3^Y - Q_1^Y = 33,3 - 17,5 = 15,8\\\Delta _Q^Z = Q_3^Z - Q_1^Z = 33,75 - 26,25 = 7,5\end{array}\)
Vì \(\Delta _Q^Y > \Delta _Q^Z\) nên nhiệt độ của địa phương Z ít biến động hơn.
