Hoạt động (HĐ) 1
Bảng 3.13 là mẫu số liệu ghép nhóm về lương của 40 nhân viên công ty M mà anh Bình có:
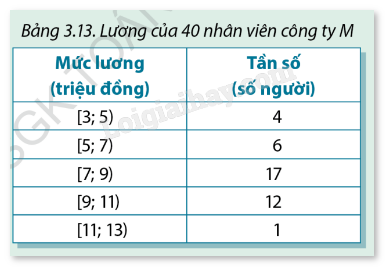
a) Hãy ước tính lương trung bình \({\overline X _M}\) của 40 nhân viên.
b) Điều anh Bình quan tâm là độ lệch trung bình giữa lương của mỗi nhân viên so với lương trung bình \({\overline X _M}\). Anh Bình có thể ước lượng độ lệch giữa lương của những nhân viên thuộc nhóm thứ nhất (nhóm lương từ 3 đến dưới 5 triệu đồng) so với số trung bình qua giá trị nào?
c) Dựa vào công thức tính trung bình của mẫu số liệu ghép nhóm và hai công thức tính phương sai, độ lệch chuẩn của mẫu số liệu không ghép nhóm, hãy đề xuất một cách ước tính phương sai và độ lệch chuẩn của mẫu số liệu gốc mà anh Bình không có (bảng lương của từng người).

a) Công thức tính điểm trung bình
\({\bar X_M} = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{n_i}} \right)} }}{N}\), trong đó:
- \({x_i}\) là giá trị đại diện của khoảng lương thứ \(i\).
- \({n_i}\) là tần số của khoảng lương thứ \(i\).
- \(N\) là tổng số nhân viên.
b) Sử dụng giá trị trung bình của nhóm lương từ 3 đến dưới 5 triệu đồng.
Công thức:
\(\Delta = \left| {{x_{[3;5)}} - {{\overline X }_M}} \right|\)
c)
- Công thức tính phương sai của mẫu số liệu không ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^N {({x_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)

a) Tính lương trung bình \({\overline X _M}\):
\(\begin{array}{l}[3;5):\frac{{3 + 5}}{2} = 4;\\(5;7):\frac{{5 + 7}}{2} = 6{\rm{ }};\\(7;9):\frac{{7 + 9}}{2} = 8{\rm{ }};\\(9;11)\frac{{9 + 11}}{2} = 10{\rm{ }};\\(11;13)\frac{{11 + 13}}{2} = 12{\rm{ }}\end{array}\)
Lương trung bình:
\({\overline X _M} = \frac{{\sum {{x_i}.{n_i}} }}{N} = \frac{{4.4 + 6.6 + 8.17 + 10.12 + 12.1}}{{40}} = 8\)
b) Ước lượng độ lệch trung bình:
Giá trị đại diện của nhóm thứ nhất (3 đến 5 triệu đồng): 4 triệu đồng
Độ lệch giữa lương của nhóm này và lương trung bình là:
\(\Delta = \left| {{x_{[3;5)}} - {{\overline X }_M}} \right| = \left| {4 - 8} \right| = 4\) triệu đồng
c)
Công thức tính trung bình là
\({\bar X_M} = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{n_i}} \right)} }}{N}\)
Công thức tính phương sai của mẫu số liệu không ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^N {({x_i}} - \overline x {)^2}\)
Ta biết rằng các giá trị \({x_i}\) nằm trong các nhóm, và mỗi nhóm có trung điểm \({x_j}\) và tần số \({n_j}\). Do đó, ta có thể viết lại tổng trên bằng cách thay thế từng \({x_i}\) trong mỗi nhóm bằng trung điểm \({x_j}\):
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^N {({x_i}} - \overline x {)^2} = \frac{1}{N}\sum\limits_{j = 1}^k {\sum\limits_{i = 1}^{{n_j}} {{{({x_i} - \overline x )}^2}} } = \frac{1}{N}\sum\limits_{j = 1}^k {{n_j}({x_j}} - \overline x {)^2}\)
Vậy công thức tính phương sai của mẫu số liệu ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{j = 1}^k {{n_j}({x_j}} - \overline x {)^2}\)
Và độ lệch chuẩn của mẫu số liệu ghép nhóm vẫn là:
\(S = \sqrt {{S^2}} \).
Luyện tập (LT) 1
Bảng dưới đây tổng hợp thời gian hoàn thành bài kiểm tra IQ của 50 học sinh lớp 9:

Tính trung bình và độ lệch chuẩn của mẫu số liệu đã cho. Nêu ý nghĩa của kết quả tìm được.

Áp dụng các công thức tính trung bình và độ lệch chuẩn của mẫu số liệu ghép nhóm:
- Công thức tính trung bình là
\(\overline x = \frac{{\sum\limits_{i = 1}^k {\left( {{c_i}{n_i}} \right)} }}{N}\)
- Công thức tính phương sai của mẫu số liệu ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^k {{n_i}({c_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)

Kích thước của mẫu số liệu là N = 50.
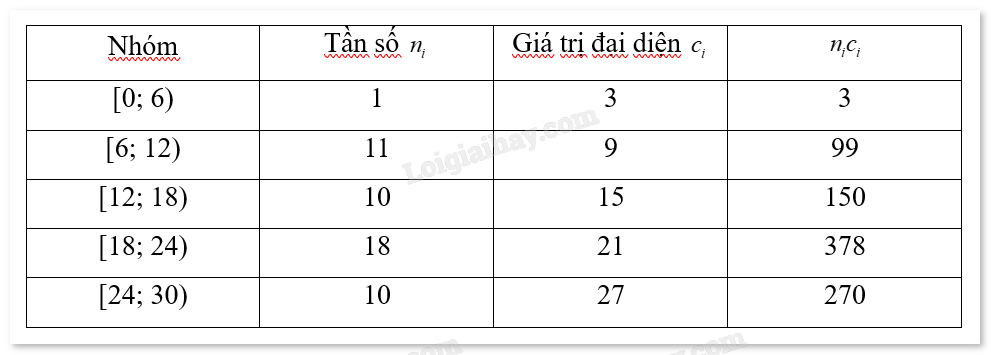
Vì có 5 nhóm nên k = 5. Trung bình mẫu:
\(\overline x = \frac{{\sum\limits_{i = 1}^5 {\left( {{c_i}{n_i}} \right)} }}{N} = \frac{{{c_1}{n_1} + {c_2}{n_2} + {c_3}{n_3} + {c_4}{n_4} + {c_5}{n_5}}}{N} = \frac{{3 + 99 + 150 + 378 + 270}}{{50}} = 18\)
Phương sai của mẫu số liệu:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^5 {{n_i}({c_i}} - \bar x{)^2} = \frac{{1.{{(3 - 18)}^2} + 11.{{(9 - 18)}^2} + 10.{{(15 - 18)}^2} + 18.{{(21 - 18)}^2} + 10.{{(27 - 18)}^2}}}{{50}} = \frac{{1089}}{{25}} = 43,56\)
Độ lệch chuẩn là:
Advertisements (Quảng cáo)
\(S = \sqrt {{S^2}} = \sqrt {43,56} = 6,6\) Các kết quả vừa tìm được cho thấy thời gian làm bài kiểm tra IQ của các học sinh lớp 9 có sự chênh lệch khoảng 6,6 so với thời gian trung bình.
Luyện tập (LT) 2
Số tiền ghi trên hoá đơn của 150 khách hàng lấy ngẫu nhiên trong một ngày được siêu thị ghi lại ở bảng dưới đây:

Tìm phương sai, độ lệch chuẩn của mẫu số liệu về số tiền ghi trên hoá đơn.

- Công thức tính phương sai của mẫu số liệu ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^k {{n_i}({c_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)

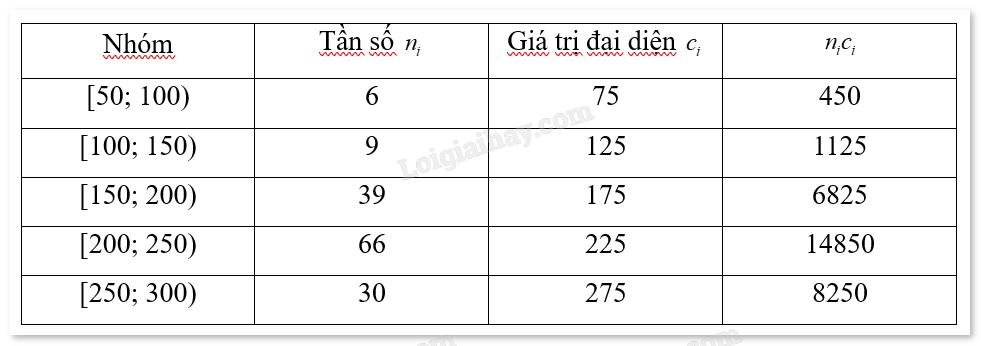
Vì có 5 nhóm nên k = 5. Số tiền trung bình:
\(\overline x = \frac{{\sum\limits_{i = 1}^5 {\left( {{c_i}{n_i}} \right)} }}{N} = \frac{{{c_1}{n_1} + {c_2}{n_2} + {c_3}{n_3} + {c_4}{n_4} + {c_5}{n_5}}}{N} = \frac{{450 + 1125 + 6825 + 14850 + 8250}}{{150}} = 210\)
Phương sai của mẫu số liệu:
\(\begin{array}{l}{S^2} = \frac{1}{N}\sum\limits_{i = 1}^5 {{n_i}({c_i}} - \bar x{)^2}\\{S^2} = \frac{{6.{{(75 - 210)}^2} + 9.{{(125 - 210)}^2} + 39.{{(175 - 210)}^2} + 66.{{(225 - 210)}^2} + 30.{{(275 - 210)}^2}}}{{150}} = 2425\end{array}\)
Độ lệch chuẩn là:
\(S = \sqrt {2425} \approx 49,24\)
Vận dụng (VD) 1
Bộ phận kiểm tra chất lượng sản phẩm dùng máy để đo (chính xác đến 0,001 mm) độ dày của một chi tiết máy. Kết quả đo một số sản phẩm được thống kê trong bảng sau:

a) Tính phương sai và độ lệch chuẩn của độ dày chi tiết máy.
b) Giải thích tầm quan trọng của việc có độ lệch chuẩn nhỏ trong trường hợp này.

a)
- Công thức tính phương sai:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^k {{n_i}({c_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)
b) Độ lệch chuẩn càng nhỏ chứng tỏ các giá trị đo được càng gần với giá trị trung bình, nghĩa là độ chính xác của máy đo cao hơn. Trong trường hợp này, độ dày chi tiết máy càng đồng nhất thì chất lượng sản phẩm càng cao.

a)
Kích thước của mẫu số liệu là: \(N = 3 + 7 + 23 + 25 + 2 = 60\)
Độ dày trung bình:
\(\overline x = \frac{{{c_1}{n_1} + {c_2}{n_2} + {c_3}{n_3} + {c_4}{n_4} + {c_5}{n_5}}}{N} = \frac{{18,5.3 + 19,5.7 + 20,5.23 + 21,5.25 + 22,5.2}}{{60}} = 20,77\)
Phương sai của mẫu số liệu:
\(\begin{array}{l}{S^2} = \frac{{3.{{(18,5 - 20,77)}^2} + 7.{{(19,5 - 20,77)}^2} + 23.{{(20,5 - 20,77)}^2} + 25.{{(21,5 - 20,77)}^2} + 2.{{(22,5 - 20,77)}^2}}}{{60}}\\{S^2} \approx 0,79557\end{array}\).
Độ lệch chuẩn là:
\(S = \sqrt {0,79557} \approx 0,89195\)
Tầm quan trọng của việc có độ lệch chuẩn nhỏ trong trường hợp này chính là: Độ lệch chuẩn nhỏ chứng tỏ các giá trị đo độ dày của chi tiết máy không bị phân tán nhiều, đảm bảo tính đồng nhất và chất lượng sản phẩm.
Vận dụng (VD) 2
Trở lại với vấn đề của anh Bình.
Ta đã biết bảng 3.13 là số liệu anh Bình có về lương của 40 nhân viên có tuổi nghề dưới 5 năm thuộc công ty M. Để tiện tính toán, ta chép lại dưới đây bảng 3.13. Đối với công ty N, anh Bình cũng thu thập được một số mẫu số liệu ghép nhóm về lương của 42 nhân viên có tuổi nghề dưới 5 năm (Bảng 3.20).
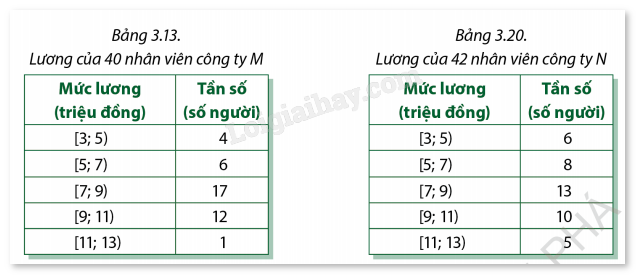
Nếu muốn làm việc ở nơi mà lương giữa các nhân viên có tuổi nghề dưới 5 năm chênh lệch nhau ít hơn thì anh Bình nên chọn công ty M hay N?

- Tính mức lương trung bình của từng nhóm nhân viên theo công thức:
\(\overline L = \frac{{\sum {{f_i}.{L_i}} }}{{\sum {{f_i}} }}\)
Trong đó \({f_i}\) là số lượng nhân viên trong nhóm với mức lương \({L_i}\).
- Tìm độ lệch chuẩn của mức lương trong từng công ty và so sánh.
\(S = \sqrt {\frac{{\sum {{f_i}.\left( {{L_i} - \overline L } \right)} }}{{\sum {{f_i}} }}} \)

Mức lương trung bình của hai công ty là:
\({\overline L _M} = \frac{{\sum {{f_i}} .{L_i}}}{{{f_M}}} = \frac{{4.4 + 6.6 + 8.17 + 10.12 + 12.1}}{{40}} = 8\)
\({\overline L _N} = \frac{{\sum {{f_i}} .{L_i}}}{{{f_N}}} = \frac{{4.6 + 6.8 + 8.13 + 10.10 + 12.5}}{{42}} = 8\)
Độ lệch chuẩn mức lương của hai công ty là:
\({S_M} = \sqrt {\frac{{\sum {{f_i}.\left( {{L_i} - {{\bar L}_M}} \right)} }}{{{f_M}}}} = \sqrt {\frac{{4.{{(4 - 8)}^2} + 6.{{(6 - 8)}^2} + 17.{{(8 - 8)}^2} + 12.{{(10 - 8)}^2} + 1.{{(12 - 8)}^2}}}{{40}}} \approx 1,95\)
\({S_N} = \sqrt {\frac{{\sum {{f_i}.\left( {{L_i} - {{\bar L}_N}} \right)} }}{{{f_N}}}} = \sqrt {\frac{{6.{{(4 - 8)}^2} + 8.{{(6 - 8)}^2} + 13.{{(8 - 8)}^2} + 10.{{(10 - 8)}^2} + 5.{{(12 - 8)}^2}}}{{42}}} \approx 2,43\)
Nhận thấy độ lệch so với mức lương của công ty N cao hơn công ty M.
Như vậy, nếu muốn làm việc ở nơi mà lương giữa các nhân viên có tuổi nghề dưới 5 năm thì nên chọn công ty M.
