Bài 3. Bước sóng của vạch quang phổ thứ nhất trong dãy Lai-man là \({\lambda _0}= 122\) nm, của hai vạch \({H_\alpha },{H_\beta }\) lần lượt là \({\lambda _1} = 0,656\mu m\) và \({\lambda _2} = 0,486\mu m\). Hãy tính bước sóng hai vạch tiếp theo trong dãy Lai-man và vạch đầu tiên trong dãy Pa-sen.
Giải
Để giải bài toán nguyên tử Hidrô, ta lưu ý sử dụng tốt sơ đồ chuyển mức năng lượng như sau:
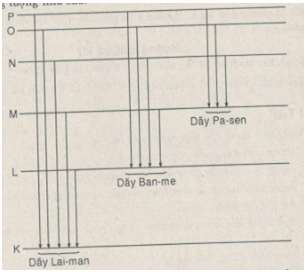
Chú ý : Vạch thứ nhất ở mỗi dãy ứng với hiệu mức năng lượng thấp nhất và bước sóng của bức xạ phát ra là lớn nhất.
Theo giả thiết : Vạch thứ nhất trong dãy Lai-man là \({\lambda _0} = {\lambda _{LK}} = 122(nm)\)
Vạch thứ nhất và vạch thứ hai trong dãy Ban-me là
\({\lambda _1} = {\lambda _{ML}} = 0,656(\mu m)\) và \({\lambda _2} = {\lambda _{NL}} = 0,486(\mu m)\)
a) Bước sóng của hai vạch tiếp theo trong dãy Lai-man là : \({\lambda _{MK}}\) và \({\lambda _{NK}}\)
Theo tiên đề Bo : \({\varepsilon _{MK}} = {E_M} - {E_K} = {E_M} - {E_L} + {E_L} - {E_K}\)
\( \Rightarrow {\varepsilon _{MK}} = {\varepsilon _{ML}} + {\varepsilon _{LK}} \Leftrightarrow {{hc} \over {{\lambda _{MK}}}} = {{hc} \over {{\lambda _{ML}}}} + {{hc} \over {{\lambda _{LK}}}}\)
Advertisements (Quảng cáo)
\( \Leftrightarrow {1 \over {{\lambda _{MK}}}} = {1 \over {{\lambda _{ML}}}} + {1 \over {{\lambda _{LK}}}} = {1 \over {0,656}} + {1 \over {0,122}}\)
\( \Rightarrow {\lambda _{MK}} = 0,1029(\mu m)\)
Tương tự :
\({\varepsilon _{NK}} = {E_N} - {E_K} = {E_N} - {E_L} + {E_L} - {E_K} = {\varepsilon _{NL}} + {\varepsilon _{LK}}\)
\( \Leftrightarrow {1 \over {{\lambda _{NK}}}} = {1 \over {{\lambda _{NL}}}} + {1 \over {{\lambda _{LK}}}} = {1 \over {0,486}} + {1 \over {0,122}}\)
\( \Rightarrow {\lambda _{NK}} = 0,0975\left( {\mu m} \right)\)
b) Bước sóng của vạch đầu tiên trong dãy Pasen :\({\lambda _{NM}}\)
Ta có :
\({\varepsilon _{NM}} = {E_N} - {E_M} = \left( {{E_N} - {E_K}} \right) - \left( {{E_M} - {E_K}} \right) = {\varepsilon _{NK}} - {\varepsilon _{MK}}\)
\( \Rightarrow {1 \over {{\lambda _{NM}}}} = {1 \over {{\lambda _{NK}}}} - {1 \over {{\lambda _{MK}}}} = {1 \over {0,0975}} - {1 \over {0,1029}} \Rightarrow {\lambda _{NM}} = 1,858(\mu m)\)
