Câu 1
Trả lời câu hỏi 1 trang 17
Quy đồng mẫu số các phân số sau:


a) Khi quy đồng mẫu số của hai phân số mà mẫu số lớn chia hết cho mẫu số bé, ta làm như sau:
- Lấy mẫu số lớn hơn là mẫu số chung
- Lấy mẫu số chung chia cho mẫu số bé
- Nhân cả tử số và mẫu số của phân số có mẫu số bé với thương vừa tìm được
b, c) Khi quy đồng mẫu số của hai phân số mà mẫu số này không chia hết cho mẫu số kia, ta làm như sau:
- Chọn mẫu số chung là tích của hai mẫu số đã cho;
- Nhân cả tử số và mẫu số của phân số thứ nhất với mẫu số của phân số thứ hai;
- Nhân cả tử số và mẫu số của phân số thứ hai với mẫu số của phân số thứ nhất;
Ta nhận được hai phân số có cùng mẫu số.

a) Mẫu số chung là 9
$\frac{1}{3} = \frac{{1 \times 3}}{{3 \times 3}} = \frac{3}{9}$; giữ nguyên $\frac{5}{9}$
Quy đồng mẫu số hai phân số $\frac{1}{3}$và $\frac{5}{9}$ ta được $\frac{3}{9}$và $\frac{5}{9}$
b) Mẫu số chung là 63
$\frac{5}{7} = \frac{{5 \times 9}}{{7 \times 9}} = \frac{{45}}{{63}}$; $\frac{{11}}{9} = \frac{{11 \times 7}}{{9 \times 7}} = \frac{{77}}{{63}}$
Quy đồng mẫu số hai phân số $\frac{5}{7}$ và$\frac{{11}}{9}$ ta được $\frac{{45}}{{63}}$ và $\frac{{77}}{{63}}$
c) Mẫu số chung là 10 : 2 × 5 = 60
$\frac{{11}}{{10}} = \frac{{11 \times 6}}{{10 \times 6}} = \frac{{66}}{{60}}$;$\frac{7}{{12}} = \frac{{7 \times 5}}{{12 \times 5}} = \frac{{35}}{{60}}$
Quy đồng mẫu số các phân số $\frac{{11}}{{10}}$ và $\frac{7}{{12}}$ ta được $\frac{{66}}{{60}}$ và $\frac{{35}}{{60}}$
Câu 2
Trả lời câu hỏi 2 trang 17
< , > , = ?
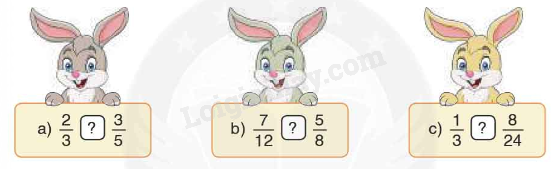

Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đã cho rồi so sánh hai phân số mới có cùng mẫu số.
Advertisements (Quảng cáo)

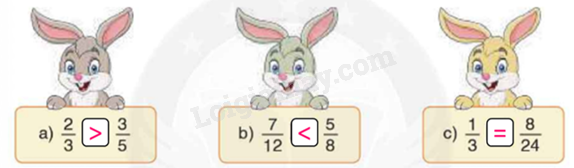
a) Ta có: $\frac{2}{3} = \frac{{10}}{{15}};\frac{3}{5} = \frac{9}{{15}}$
Nên $\frac{2}{3} > \frac{9}{{15}}$
b) Ta có: $\frac{7}{{12}} = \frac{{28}}{{48}};\frac{5}{8} = \frac{{30}}{{48}}$
Nên $\frac{7}{{12}} < \frac{{30}}{{48}}$
c) $\frac{1}{3} = \frac{8}{{24}}$
Câu 3
Trả lời câu hỏi 3 trang 17
Sắp xếp các phân số sau theo thứ tự từ bé đến lớn:


So sánh các phân số rồi sắp xếp theo thứ tự từ bé đến lớn

a) Ta có: $\frac{5}{2} = \frac{{5 \times 9}}{{2 \times 9}} = \frac{{45}}{{18}}$;$\frac{2}{3} = \frac{{2 \times 6}}{{3 \times 6}} = \frac{{12}}{{18}}$; giữ nguyên $\frac{3}{{18}}$
Mà $\frac{3}{{18}} < \frac{{12}}{{18}} < \frac{{45}}{{18}}$
Vậy các phân số sắp xếp theo thứ tự từ bé đến lớn là: $\frac{3}{{18}};\frac{2}{3};\frac{5}{2}$
b) Ta có: $\frac{5}{4} = \frac{{5 \times 3}}{{4 \times 3}} = \frac{{15}}{{12}}$;$\frac{5}{3} = \frac{{5 \times 4}}{{3 \times 4}} = \frac{{20}}{{12}}$; giữ nguyên $\frac{7}{{12}}$
Mà $\frac{7}{{12}} < \frac{{15}}{{12}} < \frac{{20}}{{12}}$
Vậy các phân số sắp xếp theo thứ tự từ bé đến lớn là: $\frac{7}{{12}};\frac{5}{4};\frac{5}{3}$
Câu 4
Trả lời câu hỏi 4 trang 17
Trường Phổ thông Dân tộc nội trú Vừ A Dính có $\frac{3}{{10}}$số học sinh là người dân tộc H’Mông, $\frac{1}{2}$ số học sinh là người dân tộc Thái và $\frac{1}{5}$ số học sinh là người dân tộc Dao. Hỏi trường đó có số học sinh là người dân tộc nào nhiều nhất?

- Quy đồng mẫu số các phân số.
- So sánh các phân số để trả lời câu hỏi.

Ta có: $\frac{1}{2} = \frac{{1 \times 5}}{{2 \times 5}} = \frac{5}{{10}}$;$\frac{1}{5} = \frac{{1 \times 2}}{{5 \times 2}} = \frac{2}{{10}}$
Mà $\frac{5}{{10}} > \frac{3}{{10}} > \frac{2}{{10}}$
Vậy trường đó có số học sinh là người dân tộc Thái nhiều nhất.
