Câu 1
Trả lời câu hỏi 1 trang 19
Tính:


Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số rồi cộng hai phân số đã quy đồng.

a) $\frac{5}{8} + \frac{3}{5} = \frac{{25}}{{40}} + \frac{{24}}{{40}} = \frac{{49}}{{40}}$
b) $\frac{2}{5} + \frac{2}{7} = \frac{{14}}{{35}} + \frac{{10}}{{35}} = \frac{{24}}{{35}}$
c) $\frac{1}{5} + \frac{2}{3} = \frac{3}{{15}} + \frac{{10}}{{15}} = \frac{{13}}{{15}}$
Câu 2
Trả lời câu hỏi 2 trang 19
Rút gọn rồi tính:
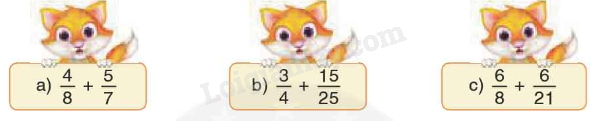

Khi rút gọn phân số ta có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1
- Chia cả tử số và mẫu số cho số đó
Cứ làm như thế cho đến khi nhận được phân số tối giản

a) $\frac{4}{8} + \frac{5}{7} = \frac{1}{2} + \frac{5}{7} = \frac{7}{{14}} + \frac{{10}}{{14}} = \frac{{17}}{{14}}$
b) $\frac{3}{4} + \frac{{15}}{{25}} = \frac{3}{4} + \frac{3}{5} = \frac{{15}}{{20}} + \frac{{12}}{{20}} = \frac{{27}}{{20}}$
c) $\frac{6}{8} + \frac{6}{{21}} = \frac{3}{4} + \frac{2}{7} = \frac{{21}}{{28}} + \frac{8}{{28}} = \frac{{29}}{{28}}$
Câu 3
Trả lời câu hỏi 3 trang 19
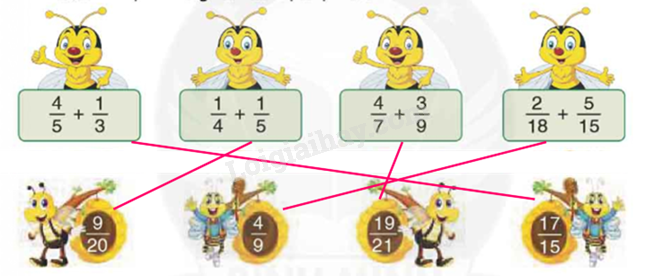
Chọn kết quả đúng cho mỗi phép tính sau:


Tính kết quả của mỗi phép tính rồi nối với kết quả đúng.

Advertisements (Quảng cáo)
Câu 4
Trả lời câu hỏi 4 trang 19
Tính bằng cách thuận tiện:
a) $\frac{3}{4} + \frac{1}{3} + \frac{1}{4}$
b) $\frac{4}{7} + \frac{3}{2} + \frac{3}{7}$

Áp dụng tính chất giao hoán và kết hợp của phân số để tính.

a) $\frac{3}{4} + \frac{1}{3} + \frac{1}{4} = \left( {\frac{3}{4} + \frac{1}{4}} \right) + \frac{1}{3} = 1 + \frac{1}{3} = \frac{3}{3} + \frac{1}{3} = \frac{4}{3}$
b) $\frac{4}{7} + \frac{3}{2} + \frac{3}{7} = \left( {\frac{4}{7} + \frac{3}{7}} \right) + \frac{3}{2} = 1 + \frac{3}{2} = \frac{2}{2} + \frac{3}{2} = \frac{5}{2}$
Câu 5
Trả lời câu hỏi 5 trang 19
Chọn đáp án đúng:
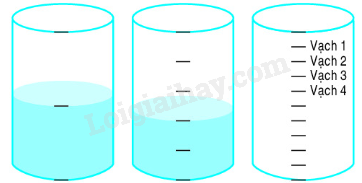
Có ba bình đựng nước kích thước như nhau, bình thứ nhất và bình thứ hai có chứa nước và bình thứ ba chưa có chứa nước (hình bên). Hỏi nếu đổ hết nước cả hai bình đầu vào bình thứ ba, thì mực nước ở bình thứ ba sẽ chạm tới vạch chia nào?
A. Vạch 1
B. Vạch 2
C. Vạch 3
D. Vạch 4

Xác định số phần lượng nước ổ bình thứ nhất và bình thứ hai so với số phần bình thứ ba.

Ta thấy: Các bình đựng nước có kích thước như nhau
Bình thứ nhất: Lượng nước = $\frac{1}{2}$ bình
Bình thứ hai: Lượng nước = $\frac{2}{5}$ bình
Vậy nếu đổ hết nước cả hai bình đầu vào bình thứ 3 thì lượng nước chiếm số phần của bình là:
$\frac{1}{2}$ + $\frac{2}{5}$= $\frac{9}{{10}}$ (bình)
Các vạch chia bình thứ ba thành 10 phần bằng nhau.
Vậy mực nước ở bình thứ ba sẽ chạm tới vạch 1.
Chọn A.
