Luyện tập 1 Câu 1
Dưới đây là số tiền điện tháng Hai của ba công ty ở một tòa văn phòng.

a) Đọc số tiền điện tháng Hai của các công ty.
b) Nêu giá trị của chữ số 3 trong mỗi số tiền trên. c) Làm tròn đến hàng nghìn số tiền điện tháng Hai của các công ty.

a) Đọc số tự nhiên: Đọc số theo các lớp, từ trái sang phải: Với mỗi lớp, ta đọc như đọc các số có một, hai hoặc ba chữ số rồi kèm theo tên lớp.
Chú ý: Để cho gọn, ta có thể không đọc tên lớp đơn vị.
b) Xác định vị trí của chữ số 3 trong mỗi số đó rồi ghi giá trị tương ứng của chữ số đó.
c) Khi làm tròn số đến hàng nghìn, ta so sánh chữ số hàng trăm với 5. Nếu chữ số hàng trăm bé hơn 5 thì làm tròn xuống, còn lại thì làm tròn lên.


a)
Số 105 362 480 đọc là: một trăm linh năm triệu ba trăm sáu mươi hai nghìn bốn trăm tám mươi.
Số 83 965 724 đọc là: tám mươi ba triệu chín trăm sáu mươi năm nghìn bảy trăm hai mươi bốn.
Số 121 783 907 đọc là: một trăm hai mươi mốt triệu bảy trăm tám mươi ba nghìn chín trăm linh bảy.
b)
Chữ số 3 trong số 105 362 480 thuộc hàng trăm nghìn nên có giá trị là 300 000.
Chữ số 3 trong số 83 965 724 thuộc hàng triệu nên có giá trị là 3 000 000.
Chữ số 3 trong số 121 783 907 thuộc hàng nghìn nên có giá trị là 3 000.
c)
Số 105 362 480 làm tròn đến hàng nghìn thành 105 362 000 vì 4
Số 83 965 724 làm tròn đến hàng nghìn thành 83 966 000 vì 7 > 5.
Số 121 783 907 làm tròn đến hàng nghìn thành 121 784 000 vì 9 > 5.
Luyện tập 1 Câu 2
a) Viết mỗi số 81 063, 40 725, 507 689, 2 640 530 thành tổng (theo mẫu).
Mẫu: 81 063 = 80 000 + 1 000 + 60 + 3
b) Số?
50 000 + 7 000 + 300 + ? + 6 = 57 346
800 000 + 40 000 + ? + 200 + 90 = 843 290

a) Xác định số trăm, số chục, số đơn vị của mỗi số rồi viết số thành tổng các trăm, chục đơn vị.
b) Điền số thích hợp vào chỗ chấm.

a)
40 725 = 40 000 + 700 + 20 + 5.
507 689 = 500 000 + 7 000 + 600 + 80 + 9.
2 640 530 = 2 000 000 + 600 000 + 40 000 + 500 + 30.
b)
50 000 + 7 000 + 300 + 40 + 6 = 57 346
800 000 + 40 000 +3 000+ 200 + 90 = 843 290
Luyện tập 1 Câu 3
Chọn câu trả lời đúng.
a) Bốn số nào dưới đây tạo thành bốn số tự nhiên liên tiếp?
A. 999; 1000; 1 002; 1 003
B. 1 958; 1 959; 1 960; 1 961
C. 4 080; 4 081; 4 082; 4 084
C. 2 587; 2 589; 2 590; 2 591
b) Bốn số nào dưới đây tạo thành bốn số lẻ liên tiếp?
A. 5 643; 5 645; 5 647; 5 651
B. 8 009; 8 011; 8 015; 8 017
C. 7 497; 7 499; 7 501; 7 503
D. 6 525; 6 529; 6 531; 6 533

a) Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị.
b) Hai số lẻ liên tiếp hơn kém nhau 2 đơn vị.

a) Chọn đáp án B.
b) Chọn đáp án C.
Luyện tập 1 Câu 4
Cho biết số dân vào giữa năm 2021 của một số nước Đông Nam Á (theo Niên giám thống kê năm 2021) như sau:
Việt Nam: 98 500 000 người
Xin-ga-po: 5 700 000 người
In-đô-nê-xi-a: 275 100 000 người
Phi-líp-pin: 110 200 000 người
a) Trong các nước trên, nước nào có số dân ít nhất, nước nào có số dân nhiều nhất?
b) Viết tên các nước trên theo thứ tự có số dân từ nhiều nhất đến ít nhất.

So sánh số dân của các nước và trả lời câu hỏi.

a) Vì 5 700 000
b) In-đô-nê-xi-a, Phi-líp-pin, Việt Nam, Xin-ga-po.
Luyện tập 1 Câu 5
Số?
a) Số tự nhiên bé nhất là ?.
b) Số lớn nhất có bảy chữ số khác nhau là ?.
c) Số bé nhất có sáu chữ số khác nhau là ?.
d) Số liền sau của số lớn nhất có bảy chữ số là ?.

Điền số thích hợp vào chỗ trống.

a) Số tự nhiên bé nhất là 0.
b) Số lớn nhất có bảy chữ số khác nhau là 9 999 999.
c) Số bé nhất có sáu chữ số khác nhau là 102 345.
d) Số liền sau của số lớn nhất có bảy chữ số là 10 000 000.
Luyện tập 2 Câu 1
a) Viết rồi đọc phân số chỉ phần đã tô màu của mỗi hình dưới đây.
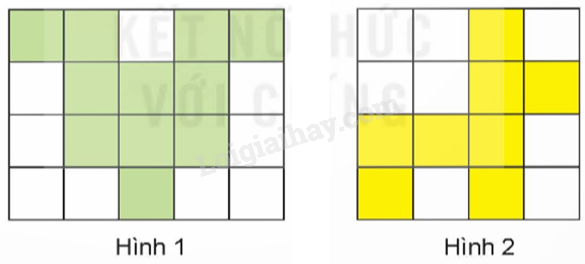
b) Viết rồi đọc hỗn số chỉ phần đã tô màu của mỗi hình dưới đây.

a)
- Quan sát hình vẽ để viết phân số tương ứng với mỗi hình.
- Trong mỗi phân số, tử số chỉ số phần bằng nhau đã được tô màu và mẫu số chỉ tổng số phần bằng nhau.
b) Khi đọc (hoặc viết) hỗn số ta đọc (hoặc viết) phần nguyên rồi đọc (hoặc viết) phần phân số.

a)
Hình 1:
- Viết: $\frac{{11}}{{20}}$
- Đọc: Mười một phần hai mươi.
Hình 2:
- Viết:$\frac{8}{{16}}$
- Đọc: Tám phần mười sáu.
b)
Hình 1:
- Viết: $2\frac{2}{3}$
- Đọc: Hai hai phần ba.
Hình 2:
- Viết: $1\frac{4}{9}$
- Đọc: Một bốn phần chín.
Luyện tập 2 Câu 2
Rút gọn các phân số: $\frac{{15}}{{21}};\frac{{20}}{{35}};\frac{{72}}{{120}}.$

Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.

$\frac{{15}}{{21}} = \frac{{15:3}}{{21:3}} = \frac{5}{7}$
$\frac{{20}}{{35}} = \frac{{20:5}}{{35:5}} = \frac{4}{7}$
$\frac{{72}}{{120}} = \frac{{72:24}}{{120:24}} = \frac{3}{5}.$
Luyện tập 2 Câu 3
Quy đồng mẫu số các phân số.
Advertisements (Quảng cáo)
a) $\frac{5}{6}$ và $\frac{{37}}{{48}}$
b) $\frac{3}{4}$; $\frac{2}{5}$ và $\frac{{13}}{{20}}$

Khi quy đồng mẫu số hai phân số có thể làm như sau:
- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.

a) $\frac{5}{6}$ và $\frac{{37}}{{48}}$
Chọn mẫu số chung là 48.
Quy đồng mẫu số hai phân số ta có:
$\frac{5}{6} = \frac{{5 \times 8}}{{6 \times 8}} = \frac{{40}}{{48}}$;
$\frac{{37}}{{48}}$ giữ nguyên.
Vậy quy đồng mẫu số hai phân số $\frac{5}{6}$ và $\frac{{37}}{{48}}$ ta được hai phân số $\frac{{40}}{{48}}$ và $\frac{{37}}{{48}}$.
b) $\frac{3}{4}$; $\frac{2}{5}$ và $\frac{{13}}{{20}}$
Chọn mẫu số chung là 20.
Quy đồng mẫu số các phân số ta có:
$\frac{3}{4} = \frac{{3 \times 5}}{{4 \times 5}} = \frac{{15}}{{20}}$;
$\frac{2}{5} = \frac{{2 \times 4}}{{5 \times 4}} = \frac{8}{{20}}$;
$\frac{{13}}{{20}}$giữ nguyên.
Vậy quy đồng mẫu số các phân số $\frac{3}{4}$; $\frac{2}{5}$ và $\frac{{13}}{{20}}$ta được các phân số $\frac{{15}}{{20}}$; $\frac{8}{{20}}$ và $\frac{{37}}{{48}}$.
Luyện tập 2 Câu 4
Các bạn Mai, Việt, Nam và Rô-bốt thi giải khối ru-bích. Thời gian hoàn thành của mỗi bạn như sau:
Mai: $\frac{3}{{10}}$giờ, Việt: $\frac{1}{2}$giờ, Nam: $\frac{2}{5}$giờ, Rô-bốt: $\frac{1}{5}$ giờ.

a) Hỏi bạn nào hoàn thành giải khối ru-bích đầu tiên, bạn nào hoàn thành giải khối ru-bích cuối cùng?
b) Mai hoàn thành giải khối ru-bích trước những bạn nào?

a) So sánh thời gian hoàn thành của mỗi bạn, bạn nào có thời gian hoàn thành lớn nhất thì sẽ hoàn thành giải khối ru-bích cuối cùng.
b) So sánh thời gian hoàn thành của Mai với các bạn khác.

a) Quy đồng mẫu số các phân số: $\frac{3}{{10}}$, $\frac{1}{2}$, $\frac{2}{5}$, $\frac{1}{5}$.
Chọn mẫu số chung là 10.
Quy đồng mẫu số các phân số ta có:
$\frac{3}{{10}}$ giữ nguyên; $\frac{1}{2} = \frac{{1 \times 5}}{{2 \times 5}} = \frac{5}{{10}}$; $\frac{2}{5} = \frac{{2 \times 2}}{{5 \times 2}} = \frac{4}{{10}}$, $\frac{1}{5} = \frac{{1 \times 2}}{{5 \times 2}} = \frac{2}{{10}}$.
Vì $\frac{2}{{10}}
Vậy bạn Việt hoàn thành giải khối ru-bích cuối cùng.
b) Mai hoàn thành khối ru-bích trước Nam và Việt.
Luyện tập 2 Câu 5
Chọn câu trả lời đúng.
Phân số thập phân $\frac{{317}}{{100}}$ viết thành hỗn số là:
A. $1\frac{{217}}{{100}}$
B. $2\frac{{117}}{{100}}$
C. $3\frac{{17}}{{100}}$
D. $31\frac{7}{{100}}$

- Tính phép chia tử số cho mẫu số.
- Giữ nguyên mẫu số của phần phân số.
- Tử số bằng số dư của phép chia tử số cho mẫu số.
- Phần nguyên bằng thương của phép chia tử số cho mẫu số.

Ta có 317 : 100 = 3 dư 17
Vậy$\frac{{317}}{{100}}$ được viết thành hỗn số là $3\frac{{17}}{{100}}$.
Chọn đáp án C.
Luyện tập 3 Câu 1
Viết các phân số thập phân sau thành số thập phân. Đọc các số thập phân đó.
$\frac{{31}}{{10}};\frac{{75}}{{100}};\frac{{489}}{{100}};\frac{{6\,024}}{{1\,000}}.$

Áp dụng cách viết: $\frac{1}{{10}} = 0,1;\,\frac{1}{{100}} = 0,01;\,\frac{1}{{1\,000}} = 0,001$
Muốn đọc một số thập phân, ta đọc lần lượt từ hàng cao đến hàng thấp: trước hết đọc phần nguyên, đọc dấu “phẩy”, sau đó đọc phần thập phân.

$\frac{{31}}{{10}} = 3,1$
3,1 đọc là ba phẩy một.
$\frac{{75}}{{100}} = 0,75$
0,75 đọc là không phẩy bẩy năm.
$\frac{{489}}{{100}} = 4,89$
4,89 đọc là bốn phẩy tám mươi chín.
$\frac{{6\,024}}{{1\,000}} = 6,024$
6,024 đọc là sáu phẩy khổng hai bốn.
Luyện tập 3 Câu 2
Viết các phân số sau dưới dạng số thập phân.
$\frac{{21}}{{30}};\frac{{62}}{{200}};\frac{7}{4};\frac{5}{8}$

- Nhân hoặc chia cả tử số và mẫu số của phân số đã cho với một số thích hợp để được phân số có mẫu số là 10; 100; 1 000,…
- Áp dụng cách viết: $\frac{1}{{10}} = 0,1;\,\frac{1}{{100}} = 0,01;\,\frac{1}{{1\,000}} = 0,001$

$\frac{{21}}{{30}} = \frac{{21:3}}{{30:3}} = \frac{7}{{10}} = 0,7$
$\frac{{62}}{{200}} = \frac{{62:2}}{{200:2}} = \frac{{31}}{{100}}$
$\frac{7}{4} = \frac{{7 \times 25}}{{4 \times 25}} = \frac{{175}}{{100}} = 1,75$
$\frac{5}{8} = \frac{{5 \times 125}}{{8 \times 125}} = \frac{{625}}{{1\,000}}.$
Luyện tập 3 Câu 3
>;
16,7 ? 16,07
85,79 ? 85,8
9,80 ? 9,8
7,360 ? 7,36
0,830 ? 0,829
28,999 ? 29,001

- Số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.
- Nếu phần nguyên của hai số đó bằng nhau,thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ... đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.

16,7 > 16,07
85,79 85,8
9,80 = 9,8
7,360 = 7,36
0,830 > 0,829
28,999 > 29,001
Luyện tập 3 Câu 4
Dưới đây là số đo diện tích các căn hộ hai phòng ngủ của một tòa chung cư:
71,5 m2; 69,83 m2; 71,09 m2; 68,93 m2.
Viết các số đo diện tích trên theo thứ tự từ bé đến lớn.

So sánh các số thập phân rồi sắp xếp theo thứ tự từ bé đến lớn:
- Số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.
- Nếu phần nguyên của hai số đó bằng nhau,thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ... đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.

Vì 68,93
68,93 m2; 69,83 m2; 71,09 m2; 71,5 m2.
Luyện tập 3 Câu 5
a) Sản lượng cá đánh bắt được của công ty Thành Long trong tháng Ba gấp rưỡi tháng Hai. Vậy sản lượng cá đánh bắt được của công ty Thành Long trong tháng Ba bằng ? % tháng Hai.
b) Sản lượng cá đánh bắt được của công ty Thành Long trong tháng Tư bằng 60% tháng ba. Vậy sản lượng cá đánh bắt được của công ty Thành Long trong tháng Tư bằng ? tháng Ba.


Điền số thích hợp vào ô trống.

a) Sản lượng cá đánh bắt được của công ty Thành Long trong tháng Ba gấp rưỡi tháng Hai tức là
Sản lượng cá đánh bắt được của công ty Thành Long trong tháng Ba : Sản lượng cá đánh bắt được của công ty Thành Long trong tháng Hai = 1,5 = 150%
Vậy sản lượng cá đánh bắt được của công ty Thành Long trong tháng Ba bằng 150 % tháng Hai.
b)
Sản lượng cá đánh bắt được của công ty Thành Long trong tháng Tư bằng 60% tháng Ba tức là
Sản lượng cá đánh bắt được của công ty Thành Long trong tháng Tư : Sản lượng cá đánh bắt được của công ty Thành Long trong tháng Ba = 60% = 0,6 = $\frac{6}{{10}}$ = $\frac{3}{5}$
Vậy sản lượng cá đánh bắt được của công ty Thành Long trong tháng Tư bằng $\frac{3}{5}$tháng Ba.
