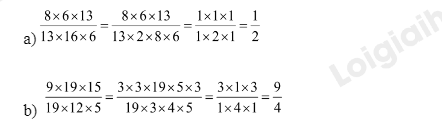Bài 3: Ôn tập phân số (tiết 1) trang 11, 12 VBT Toán 5 - Kết nối tri thức: Phân số nào dưới đây là phân số tối giản?...

Bài 1

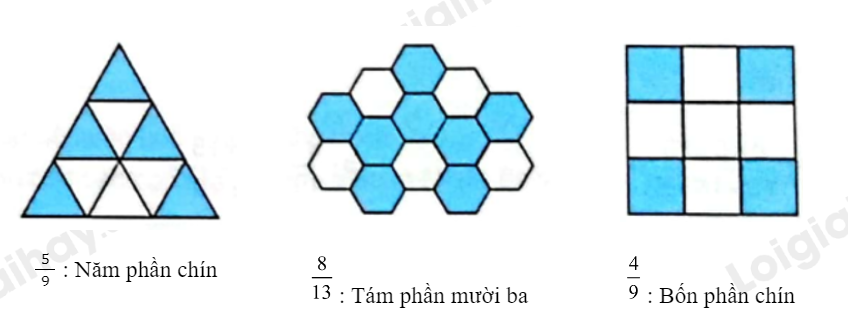
Viết phân số và cách đọc phân số chỉ số phần đã tô màu của mỗi hình (theo mẫu).

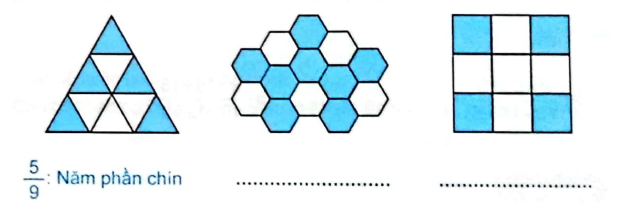
- Phân số chỉ phần đã tô màu có tử số là số phần đã tô màu, mẫu số là số phần bằng nhau.

- Khi đọc phân số ta đọc tử số trước, dấu gạch ngang đọc là “phần”, sau đó đọc mẫu số.

Bài 2

a) Viết số thích hợp vào chỗ chấm.

\(\frac{{30}}{{48}} = \frac{{...}}{{24}} = \frac{5}{{...}}\)

\(\frac{{42}}{{56}} = \frac{6}{{...}} = \frac{{...}}{4} = \frac{9}{{...}}\)

b) Rút gọn các phân số.

\(\frac{{24}}{{36}} = .......\)

\(\frac{{56}}{{70}} = .......\)

\(\frac{{64}}{{96}} = .......\)

a)

- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

- Nếu chia cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

b) Cách rút gọn phân số:

- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.

- Chia tử số và mẫu số cho số đó.

- Cứ làm như thế cho đến khi nhận được phân số tối giản.

a) Viết số thích hợp vào chỗ chấm.

\(\frac{{30}}{{48}} = \frac{{15}}{{24}} = \frac{5}{8}\)

\(\frac{{42}}{{56}} = \frac{6}{8} = \frac{3}{4} = \frac{9}{{12}}\)

b) Rút gọn các phân số.

\(\frac{{24}}{{36}} = \frac{{24:6}}{{36:6}} = \frac{4}{6} = \frac{{4:2}}{{6:2}} = \frac{2}{3}\)

\(\frac{{56}}{{70}} = \frac{{56:7}}{{70:7}} = \frac{8}{{10}} = \frac{{8:2}}{{10:2}} = \frac{4}{5}\)

\(\frac{{64}}{{96}} = \frac{{64:2}}{{96:2}} = \frac{{32}}{{48}} = \frac{{32:8}}{{48:8}} = \frac{4}{6} = \frac{{4:2}}{{6:2}} = \frac{2}{3}\)

Bài 3

Khoanh vào chữ đặt trước câu trả lời đúng.

a) Phân số nào dưới đây là phân số tối giản?

b) \(\frac{2}{5}\)bằng phân số chỉ phần đã tô màu của hình nào dưới đây?

a) Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn 1.

b) Phân số chỉ phần đã tô màu có tử số là số phần đã tô màu, mẫu số là số phần bằng nhau.

a) Đáp án: D

b) Đáp án: B

Bài 4

Quy đồng mẫu số các phân số.

a) \(\frac{7}{8} và \frac{{25}}{{36}}\)

b) \(\frac{{13}}{{20}} và \frac{{49}}{{80}}\)

c) \(\frac{3}{4};\frac{{11}}{{12}} và \frac{{31}}{{36}}\)

- Xác định mẫu số chung

- Tìm thương của mẫu số chung và mẫu số của phân số kia.

- Lấy thương tìm được nhân với tử số và mẫu số của phân số cần quy đồng

Bài 5

Tính.

- Chia nhẩm cả tử số và mẫu số cho các thừa số chung.