Bài 1
Viết hỗn số thích hợp vào chỗ chấm dưới vạch của tia số.
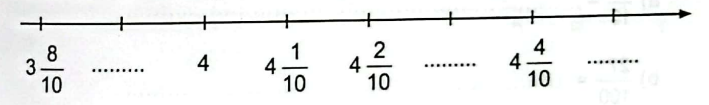

Đếm thêm \(\frac{1}{{10}}\) rồi viết hỗn số thích hợp vào chỗ trống.


Bài 2
Chuyển hỗn số thành phân số thập phân (theo mẫu).
Mẫu: \(2\frac{3}{{10}} = 2 + \frac{3}{{10}} = \frac{{23}}{{10}}\)
a) \(3\frac{1}{{10}} = ...\)
b) \(6\frac{8}{{10}} = ...\)
c) \(2\frac{9}{{100}} =...\)
d) \(1\frac{{37}}{{100}} = ...\)

Tách hỗn số thành phần nguyên cộng với phần phân số rồi tính.

a) \(3\frac{1}{{10}} = 3 + \frac{1}{{10}} = \frac{{31}}{{10}}\)
b) \(6\frac{8}{{10}} = 6 + \frac{8}{{10}} = \frac{{68}}{{10}}\)
c) \(2\frac{9}{{100}} = 2 + \frac{9}{{100}} = \frac{{209}}{{100}}\)
d) \(1\frac{{37}}{{100}} = 1 + \frac{{37}}{{100}} = \frac{{137}}{{100}}\)
Bài 3
Advertisements (Quảng cáo)
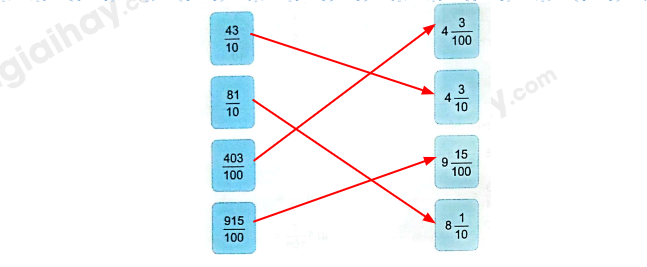
Nối phân số thập phân với hỗn số thích hợp.
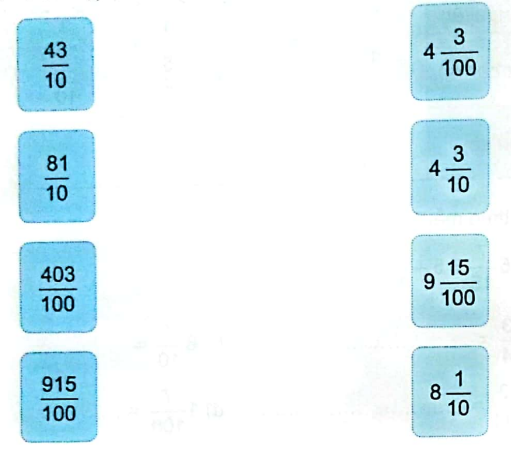

Chuyển từng hỗn số ở cột bên phải sang phân số rồi nối với ô tương ứng ở cột bên trái.

Bài 4
Viết các phân số thập phân thành hỗn số (theo mẫu).
Mẫu:\(\frac{{47}}{{10}} = \frac{{40 + 7}}{{10}} = \frac{{40}}{{10}} + \frac{7}{{10}} = 4\frac{7}{{10}}\)
a) \(\frac{{61}}{{10}} = ...\)
b) \(\frac{{271}}{{100}} = ...\)
c) \(\frac{{79}}{{10}} = ...\)
d) \(\frac{{2083}}{{1000}} = ...\)

Tách phân số thập phân thành hỗn số theo mẫu.

a) \(\frac{{61}}{{10}} = \frac{{60 + 1}}{{10}} = \frac{{60}}{{10}} + \frac{1}{{10}} = 6 + \frac{1}{{10}} = 6\frac{1}{{10}}\)
b) \(\frac{{271}}{{100}} = \frac{{200 + 71}}{{100}} = \frac{{200}}{{100}} + \frac{{71}}{{100}} = 2 + \frac{{71}}{{100}} = 2\frac{{71}}{{100}}\)
c) \(\frac{{79}}{{10}} = \frac{{70 + 9}}{{10}} = \frac{{70}}{{10}} + \frac{9}{{10}} = 7 + \frac{9}{{10}} = 7\frac{9}{{10}}\)
d) \(\frac{{2083}}{{1000}} = \frac{{2000 + 83}}{{1000}} = \frac{{2000}}{{1000}} + \frac{{83}}{{1000}} = 2 + \frac{{83}}{{1000}} = 2\frac{{83}}{{1000}}\)
