
Chứng minh định lí: “Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông”.Chứng minh định lí: “Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông”.

Hình vẽ minh họa:
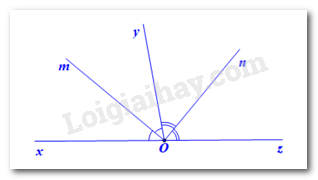
Viết giả thiết và kết luận bằng kí hiệu:

Chứng minh định lí:
Vì tia Om là tia phân giác của \(\widehat {xOy}\) nên ta có:
Advertisements (Quảng cáo)
\(\widehat {xOm}\)=\(\widehat {mOy}\)=\(\dfrac{1}{2}\)\(\widehat {xOy}\) (1)
Vì tia On là tia phân giác của \(\widehat {yOz}\) nên ta có:
\(\widehat {yOn}\)=\(\widehat {nOz}\)=\(\dfrac{1}{2}\)\(\widehat {yOz}\) (2)
Từ (1) và (2) ta có:
\(\widehat {mOy} + \widehat {yOn} = \dfrac{1}{2}\widehat {xOy} + \dfrac{1}{2}\widehat {yOz} = \dfrac{1}{2}(\widehat {xOy} + \widehat {yOz})\)
Mà \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên:
\(\widehat {xOy}\)+\(\widehat {yOz}\)=180°
Do đó \(\widehat {mOy}\)+\(\widehat {yOn}\)=\(\dfrac{1}{2}\).180°=90°
Hay \(\widehat {mOn}\)=90°.
Vậy \(\widehat {mOn}\)=90°
